问题变式：结构与功能的统一

摘要：数学问题变式可分为水平变式和垂直变式，问题变式本身展示了结构与功能的统一。

关键词：问题变式；结构；功能；认知

本文以数学问题变式为例，论述问题变式中结构与功能的统一。

近几十年来，数学学习中，问题受到了很好的注意。但很多研究更多地关注单个问题，数学问题与数学问题之间的关系，并未加以应有的关注。事实上，学生往往不是解一道题，而是解几道题，学生可能从题题之间不变的关系中抽象出数学意义，进而把问题分类，使题目类型化。变式教学是数学教师十分熟悉的教学思想、教学理念，这方面有很多实践，可理论研究还很弱。为什么该教学方法有用？变式教学的合理之处是什么？本文尝试以此为“透镜”，通过题题之间的结构，透视数学问题变式的功能。

最近，以Marton为首的欧洲学派的变式学习理论研究，逐步在香港界扎根并开花结果。Marton变式学习理论认为经历事物的方式就是学习（Marton & Booth，1997）。把“变的部分”和“不变的部分”加以区别，人们所经历的过程，称为变式学习。

一、数学教学中的问题变式

变式，可以说是内地“本土化”的实用教学经验。为了通俗地介绍变式题，笔者先从读小学时的一个小故事谈起。一位小学教师出了一道题：的是多少？当时大家都不会做。于是这位教师就说：“以后解题，凡看见××××的多少，用除法。看见××××是多少，用乘法。所以这道题用乘法。”于是我会做这类题了，却根本不懂什么意思。后来，这位数学教师继续上课，他用一串启发性的由浅入深的题组（下表），令我豁然开朗。这就是问题变式。

                题目：的倍是多少？

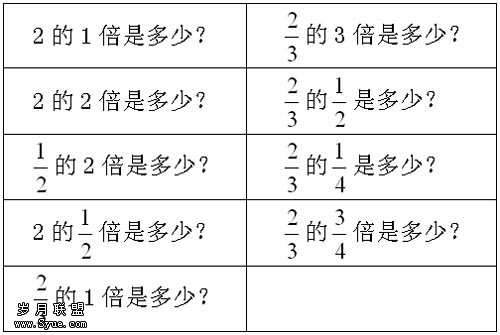
我们一般把将源问题加以变化的这些新问题，称为变式题。将源问题加以变化，称为问题变式。

二、数学问题变式的结构

（一）问题的两重特征

每个数学问题可分解为表面形式特征和深层数学结构特征。表面形式特征是指问题呈现的表述方式的浅层特征；数学结构特征指涉及问题本质的概念、关系与原则等的深层特征。

例如，25个学生一起去划船。大船每条可以坐6人，租金10元；小船每条只可以坐4人，租金8元。应该怎样租船才付最少的租金呢？要租多少条大船？多少条小船？租金又是多少呢？这个问题的表面特征是问题情境的陈述：一系列数字。这些数字，经过调换，可以变化，但是对问题的本质影响不大。至于这一题目的数学结构特征则是：题目中涉及人数、大小船数、空位数和钱数共四个变量，学生需要综合思考四个变量之间的变化依赖关系。

问题的表面特征和数学结构特征彼此相异，又互相补充。数学结构特征必须通过表面形式特征来体现，表面形式特征可以反映数学结构特征。但是，数学结构特征反映问题“质”的方面，处于核心地位。

（二）问题变式的两类结构：水平变式和垂直变式

这里，我们提出一种新的分类。新问题相对源问题来说，学生能区分问题表面形式特征变化背后的结构特征变化，不带来认知负荷的变化，为水平变式；学生不能区分问题表面形式特征变化背后的结构特征变化，带来认知负荷的变化，为垂直变式。这里我们把“问题解决过程中，记忆容量和信息加工的负荷，统称为认知负荷（cognition load）。

这样，可按问题结构的变化分成不同的层次（垂直变式），在同一结构层次中，可以分成问题表面形式特征不同的变化（水平变式）。一般来说，题目的认知负荷要在学生可理解的范围即最近区内。

例如，源问题是：2的1倍是多少？变式题1是：2的2倍是多少？

相对源问题，变式题1的水平变式部分是：2的几倍是多少？1倍变为2倍是变化的新部分，若新部分不带来认知负荷的变化，为水平变式，否则是垂直变式。

还可以有变式题2：的2倍是多少？

相对变式题1，变式题2的水平变式部分是：几的2倍是多少？2变为是变化的新部分，增加了分数概念或小数的概念以及约分的技能的认知负荷。若学生能区分问题表面形式特征变化背后的结构特征变化，不带来认知负荷的变化，为水平变式，否则是垂直变式。这种区分，以学生的感知为标准。

教学的关键是化“难”为“易”，化“垂直变式”为学生容易理解的“水平变式”，化“大变”为学生容易区分的“小变”，化“质变”为“量变”，这是数学教学的重要技能。

值得一提的是，水平变式和垂直变式的划分是相对认知水平而言的。例如，上述问题变式对小学生而言，可能有认知负荷，那么是垂直变式，而对中学生而言，可能没有认知负荷，是水平变式。两类结构的区分主要以有无认知负荷为标准。

水平变式是问题表面重复部分，垂直变式是问题表面变化部分，增加了认知负荷，二者围绕数学结构“中心轴”发展，三者（水平部分，垂直部分，数学结构“中心轴”）形成了螺旋式发展问题空间。变式教学的精髓就是把认知负荷大的问题，分解为认知负荷小的问题，把垂直变式化为螺旋，循序渐进，分解水平变式。（这即是中国数学教学的传统策略“大化小，小化了，分而治之，分散难点”的做法。）

问题变式的优势在于“渐”。变式题不同于记忆型题目和高层思维型开放题，而是在记忆型题目和高层思维型开放题两个“极端”之间保持“平衡”，渐渐地增加认知负荷，更注意题与题之间的变化，由水平变式到垂直变式，逐步区分表面形式特征并提取数学结构的元素，逐步区分题目中的数学结构的元素，发现“变中的不变”，同时培养“以不变应万变”的能力，从量变到质变，渐渐领悟，把握数学教学的（如下页图）。

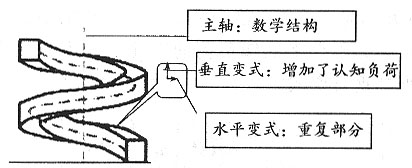
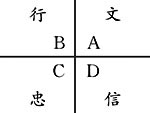
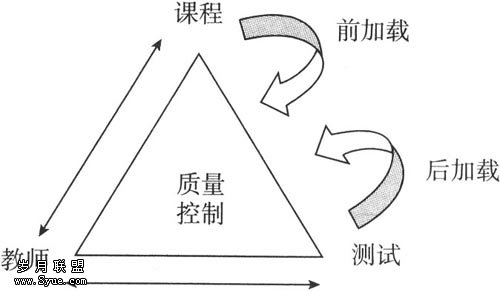
图1 问题变式结构示意图

（三）问题变式的意义

表面形式有差异的水平变式仍然有重要的价值。Marton变式学习理论认为，经验不断重复才能形成意义。重复是手段，扩展重复形成意识。第一次经历与第二次经历是互相弥补的。第一次关注理论描述效度。当第二次经历时，第一次所经历的方面被放大。第二次的经历“丰富”并“加深”第一次经历的各个方面。经历者与经验的关系只有第二次才能看到。第一次是第二次的基础，每次焦点不同，强调的方面也不同。学习经验的两个维度是直接维度（内容）和间接维度（方法）。学习是经验的“回归”方式，重复是手段，重复的意义在于保持某些方面变而其他方面不变，强调内容不变的某些方面，使其他在边缘的东西，慢慢淡化，突出主要因素，慢慢形成结构。

水平变式题虽然只是解题技能的简单重复，但量变是质变的基础，学生通过表面形式特征的重复，才能慢慢形成问题的图式，进而成为问题解决的基础。

当然，没有垂直变式题，只有水平变式是不行的。数学学习停留于浅层的学习是经验的浅层“回归”方式，不会实现深层意义的“回归”和深层结构的“回归”。按照Sfard（1991）数学概念的二重性分析，没有垂直变式题，只有水平变式，数学学习不能到达内化和浓缩化阶段，仅停留于过程性理解，难以生成概念性理解，难以生成抽象化和高层数学理解。

三、数学问题变式的功能：“概念与过程”

数学学习往往要经历“过程”达成，然后转化为“概念”（对象）的认知过程（Sfard,1991；鲍建生，等，2003）。从这个意义上，问题变式也不可避免地扮演过程的操作性和概念的结构性两重角色，鲍建生等（2003）把变式分为“概念性变式与过程性变式”正基于这种考虑。

教学上，问题变式不要无的放矢，为变而变，变式题设计总是围绕数学概念的元素和关系，分别设计区别该元素的题组，围绕“期望达成的概念和程序”而设计“问题变式题组”。变式问题，包含双重目的：概念与过程，即建构概念和技能与发展思维过程，也就是兼顾“内容和过程”，兼顾数学知识基础到高层次思维能力。

例如，我们通过这样的题目：“2个苹果，2个人分，每个人分多少个”“4个苹果，2个人分，每个人分多少个”“6个苹果，2个人分，每个人分多少个”，学习除法概念和除法运算程序。

而通过题组：“1个苹果，2个人分，每个人分多少个”“1个苹果，3个人分，每个人分多少个”“2个苹果，3个人分，每个人分多少个”，同时学习分数概念和除法运算程序。

而两者结合，题组：“个苹果，2个人分，每个人分多少个”“个苹果，2个人分，每个人分多少个”“个苹果，2个人分，每个人分多少个”，则围绕分数除法的概念和分数除法的运算程序，设计新的变式题组。而对于分数除法的概念和运算程序建立，是以“除法概念”和“分数概念”及“除法运算”和“分数运算”为基础的。

事实上，这组题目显示了发展概念和培养过程的相辅相成，具有概念与过程双重性。

因此，问题变式的，是为了概念发展的螺旋式改变而设计，通过“结构”问题产生认知“功能”，达成教学“目标”。发展数学认知结构的概念和过程的关系如下图所示。

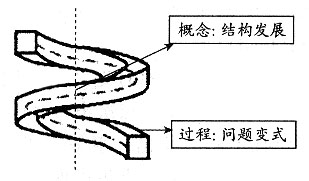
图2 问题变式的双重目的：概念与过程关系图示

四、问题变式：结构与功能的统一

在学习者眼中，变式题包含的概念（数学结构）是源题目的重复，是再认（重复性）题目，认知的功能是“巩固”，否则，垂直变式不能区分题目包含的数学概念和关系（数学结构），即增加了新的认知元素，必须区分题目的认知负荷。在学习者眼中，是发展性题目，认知的功能扮演“发展”的角色。问题变式本身展示了结构与功能的统一。我们以一个例子加以说明。

             源问题：x²+5x+6

根据一般初二学生的认知水平，变式题组一为水平变式题，变式题组二为垂直变式题^①。学生的认知过程可以作以下的描述。

1.源问题提供了问题解决的正确图式。其中包括与学习有关的关键成分：规则功能、适用条件，以及在具体情境中的操作过程。学生从源问题x²+5x+6获得十字相乘法的规则和图式认识。

2.对于可以用十字相乘法的数学结构，引出一系列的水平变式“子问题”。经过表面相似问题的解决，学习者就可能会形成一种心理定势，建立起十字相乘法的数学结构，突破源问题数字和字母的限制。

3.接着，通过垂直变式题x²+ax+6，发展原来的数学结构，建立新数学结构。对于新问题x²+ax+6，学生开始反思x²+5x+6=(x+2)(x+3)中x²+5x+6系数5和6与2和3的关系，逐步摆脱例题表面内容（系数5和6）的制约，由表层结构特征过渡到数学结构特征，突破系数的限制，认识到等号左侧一次项系数与等号右侧一次项系数的一一对应关系即a=2+3。

4.同理，通过垂直变式题x²+5x+b会努力地对问题表面特征（系数5和6）的变化进行自我解释，逐步摆脱例题表面内容（系数5和6）的制约，突破系数的限制，认识到等号左侧常数项与等号右侧常数项的一一对应关系即b=2×3［化为x²+5x+b=(x+2)(x+3)］。

5.发展高层次的结构：韦达定理，随即乘胜追击，推广到于三次、四次方程，进一步n次方程的情形。

问题变式的核心是数学结构的学习。它逐步增加认知负荷，逐步驱动高层的数学思维，逐步由表层类比（数字和字母的变化）向结构类比（因式分解的一般规则）转化。它增加了深层策略，把原来的程序知识转化为策略知识，由表层学习向结构学习转化，逐步增加输出深层结构的学习结果，逐步增加对数学本质的深层体会，逐步增加对深层数学价值的体会，使数学学习由起点（例题）到终点（垂直变式题）深层经历。

五、问题变式的问题解决过程理论小结

综上所述，变式本身是对问题结构的学习。水平变式题建立覆盖所有正例并排除所有反例的一般描述的数学结构，垂直变式是条件认知的较深层次的加工，它抽取问题表面特征以外的结构特征，不会受阻于问题的表面特征，构成题目的“结构骨架”。学习者由水平变式题到垂直变式题的解答，建立题目的数学结构，逐步由表层区分过渡到结构区分。水平变式是垂直变式的基础，垂直变式是水平变式的必然发展，二者互相依存，互为补充。

欲从水平变式“过渡到”垂直变式，关键要把握认知负荷的问题，认知负荷太大或太小，不会从水平变式“过渡到”垂直变式，好的课程设计要使题目的难度在学生的最近发展区内，变化题目的表面形式特征，同时控制不变的数学结构，最终让学生掌握“变中的不变”，培养“以不变应万变”的本领。在不断“区分”中，学习数学的“思维”，促进“表层学习向深层学习”方式的培养。课程论和方法论是不可分割的一个整体，从“结构”到“建构”，形成整体“结构”，才会产生整体“功能”。当然，变式的“度”至关重要，变的“度”太小，成了题海战术，变的“度”太大，又跳到另一个极端，学生不能掌控，产生失败感，同样不能产生高层次思维，不能产生认知“功能”。

       图3 垂直变式、水平变式与数学结构关系示意图

   

    ①对xⁿ+ax+b的分解，我们规定在有理数系下进行。这一垂直变式题组，关键在于增加了代数基本定理这一“理念”的认知负荷。

：

［1］S Blessing,B Ross.Content Effects in Problem Categorization and Problem Solving［J］.Journal of Experimental Psychology:Learning,Memory,and Cognition,1996,(22).

［2］W Doyle.Work in Mathematics Classes:The Context of Students’ Thinking during Instruction［J］.Educational Psychologist,1988,(23).

［3］P Halmos.The Heart of Mathematics［J］.American Mathematical Monthly,1980,(87).

［4］L R Novick,K J Holyoak.Mathematical Problem Solving by Analogy［J］.Journal of Experimental Psychology:Learning,Memory,and Cognition，1991.

［5］A Sfard.On the Dual Nature of Mathematics Conception:Reflections on Processes and Objects as Different Sides of the Same Coin［J］.Educational Studies in Mathematics,1991,(1).

［6］R R Skemp.The Psychology of Learning Mathematics［C］Middlesex,England:Penguin Books,1986.

［7］M K Stein,S Lane.Instructional Tasks and the Development of Student Capacity to Think and Reason:An Analysis of the Relationship between Teaching and Learning in a Reform Mathematics Project［J］.Educational Research and Evaluation，1996,(2).

［8］M K Stein,M S Smith.Mathematical Tasks as A Framework for Reflection:From Research to Practice［J］.Mathematics Teaching in the Middle School，1998,(3).

［9］Sun Xu Hua,Wong Ngai Ying,Lam Chi Chung.Bianshi Problem as the Bridge from“Entering the Way”to“Transcending the Way”:The Cultural Characteristic of Bianshi Problem in Chinese Math Education［J］.Journal of the Korea Society of Mathematical Education Series D:Research in Mathematical Education，2005,(2).

［10］J Sweller.Cognitive Load during Problem?solving:Effect on Learning［J］.Cognitive Science，1988,(2).

［11］J Sweller,Cognitive Processes and Instructional Procedures［J］.Australian Journal of Education，1990,(2).

［12］戴再平.开放题数学教学的新模式［M］.上海：上海出版社，2002.

［13］鲍建生，黄荣金，易凌峰，顾泠沅.变式教学研究［J］.数学教学，2003，（13）.