高等教育的学费标准制定问题（二）

　　4.2.2 高等层次的划分

　　目前，我们国家的高等教育一般分为研究生教育、本科生教育和专科生教育三种教育层次。通过资料查询及对数据的处理可以得到以下数据：

          表1  学历与未来年收益之间的数据关系  （单位：元）

年份         年收益 学历	2003	2004	2005	2006	2007
研究生	32436	33928	33552	35498	40332
本科生	17388	18187	18588	19666	21456
专科生	15276	15978	15996	16923	16920

　　注意：这里所说的未来年收益，是指某一学历的毕业生第一年工作的收益。

          表2   学历与年教育成本之间的关系   （单位：元）

年份          年成本 学历	2003	2004	2005	2006	2007
研究生	19499.9	19670.3	19592.1	22183.7	21329.4
本科生	10833.3	9593.5	9493.6	12923.1	12465.3
专科生	10215.4	9382.1	9248.3	10769.2	10455.6

　　由上表可知，教育层次与教育成本及其未来收益在一定程度上是成正相关的，也就是说，三个不同层次的教育将直接给受教育者带来个人预期收入的差异，随着学历的递增而递增，其成本投入也随着学历的递增而递增，甚至成倍的递增。

　　根据各教育层次的高校的生均成本的不同可以得到以下关系式：

     =  ,    =  ，且 ，j=1,2。

　　其中，

　　 表示研究生教育的生均成本占三个教育层次的生均成本之和的比重；

           表示本科生教育的生均成本占三个教育层次的生均成本之和的比重；

　　 表示专科生教育的生均成本占三个教育层次的生均成本之和的比重；

　　 表示比例系数。

　　我们通过数据资料的查找及对2003年至2007年的数据进行处理得到下表：

表4   在地区和学校类别等都相同的条件下的不同教育层次的生均成本

教育层次 生均成本	研究生教育	本科生教育	专科生教育	总计
生均培养成本  (单位：元)	20455	11061	10014	41530

　　所以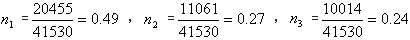

　　进一步可以得到：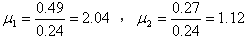

　　4.2.3      高校的类别划分

　　对于不同教育层次的高校又有不同质量的高校，根据高校的具体情况及差异，有不同的分类方法，在此我们按高校的排名将全国的高校分为甲类、乙类、丙类三类高校，其中，甲类为排名前30名的高校，乙类为排名在30至150名之间的高校，丙类为150名以后的高校。显然，这三类高校的教学设备的先进程度、教学人员的教学素养、教育资源的利用率、学生的素质和学习的环境等都有明显的差别。

   根据各个等级的高校的生均成本的不同可以得到以下关系式：

      = ，  =  ，且 ，k=1，2。

　　其中，

           表示甲类高校的生均成本占甲、乙、丙三类高校的生均成本之和的比重；

　　 表示乙类高校的生均成本占甲、乙、丙三类高校的生均成本之和的比重；

　　 表示丙类高校的生均成本占甲、乙、丙三类高校的生均成本之和的比重；

　　 表示比例系数。

　　我们通过数据资料的查找及对2003年至2007年的数据进行处理得到下表：

表5    在地区、教育层次等都相同的条件下的不同学校类别的生均成本

高校类别 生均成本	甲类高校	乙类高校	丙类高校	总计
生均培养成本 （单位：元）	13629	11173	10348	35150

　　按上述同样方法可以算得： =0.39， =0.32， =0.29；

                   =1.34，=1.11 。

　　4.2.4      专业的类别划分

　　考虑到教育质量与教育的成本，以及未来预期收益这三者之间有一定程度的正相关性，也就是说，在其它条件不变的情况下，一个学生所接受的高等教育的质量越高，对其投入的教育成本就越多，同时他个人预期的收益就越高，反之亦然。所以我们可以根据高等教育中的个人收益的高低及就业前景的好坏，将高等教育的专业分为热门专业、一般热门专业和冷门专业这三类专业。在一般情况下，毕业于热门专业的学生，其个人预期收益要比毕业于一般专业的学生的个人预期收益要高，而毕业于一般专业的学生的个人预期收益又要比毕业于冷门专业的学生的个人预期收益要高一些。

　　根据各个专业的生均成本的不同可以得到以下关系式：

        =  ， =   ，且，2。

　　其中，表示热门专业的生均成本占热门、一般、冷门三类专业的生均成本之和的比重；

　　 表示一般专业的生均成本占热门、一般、冷门三类专业的生均成本之和的比重；

　　 表示冷门专业的生均成本占热门、一般、冷门三类专业的生均成本之和的比重； 

　　 表示比例系数。

　　我们通过数据资料的查找及对2003年至2007年的数据进行处理得到下表：

表6  在地区、教育层次和学校都相同的条件下的不同专业的生均成本

专业 生均成本	热门专业	一般专业	冷门专业	总计
生均培养成本 （单位：元）	14238	11297	10073	35608

　　4.3 学费标准模型

    对于国家来说，它关注的是高等教育的质量，即国家希望教育质量更好。而教育的质量需要经费来作保障，根据前面的假设可知教育质量与教育经费之间在一定程度上有正相关性，而教育经费又决定了生均成本，所以要使教育质量更好，也就是使教育经费更多，从而可以转化为使生均成本更高，所以可得到一个目标函数：  

    , 表国家利益目标。

    对于学校来说，它关注的是在保证教育质量的前提下，有更多的经费用于自身的，据此可以得到另一个目标函数：

，   表学校利益目标。

    对于家庭（或学生）来说，关注的是对学费和生活费等的支付能力，因此，我们可以得到最后一个目标函数：

  ，    表学生家庭利益目标。

    下面我们来讨论约束条件：

    在保证教育质量的情况下，学校不能亏本，据此可得约束条件：

                   ；

　　为了满足某一家庭的学生能顺利的上学，即家庭能够提供的起学费和生活费，所以可得一约束条件：        

   

　　国家文件规定:学费不超过生均培养费的25% 。

　　所以我们可以得到以下多目标规划模型：

　　5  模型求解

　　5.1 某B区的学校作为样本来其生均培养成本

　　表7  2004年分地区中央部门普通高等学校教育经费

支出明细统计（部分）

地区	省1	省2
总计	6473510	1671129
个人部分	2562497	750430
基本工资	393084	138276
补助工资	382540	121008
其他工资	777136	172769
职工福利费	142500	23761
社会保障费	605046	206179
奖贷 助学金	262191	88437
公用部分	3041798	787659
公务费	668753	214400
业务费	351999	151434
设备购置费	678932	156350
修缮费	405489	76699
校舍建设费	113357	10664
其他费用	936625	188776
基建支出	869215	133040
自筹基建支出	668667	115330

 

    通过查询中国统计年鉴知2004年在校高校生人数为892018，

　　将上表中数据代入公式（4.1），可求出该区生均培养费为：

C= 1.477 (万元)

　　5.2 求解该样本的学费标准

　　查询中国统计年鉴可得2004年该样本的预算内教育经费为774717.633万元，从而得到生均国家拨款 B= 0.868 (万元)，Q = 0.826 (万元)。

　　考察该样本的平均每户家庭每年可支配收入J=9421.61*2.98=2.81（万元）

    20004年国内生产总值GDP=136875.9亿元 ，教育经费占GDP的百分比/* MERGEFORMAT 

　　查询数据：

    2004年A区的在校大学生年均生活消费额S=5021元 

    2004年B区的在校大学生年均生活消费额S=4637元

    下面求解多目标规划问题4.2，直接求解较复杂，应将多目标转化为单目标，然后进行求解。首先应建立三个目标函数的隶属度关系函数。隶属度在本文中指所求得的/* MERGEFORMAT 对约束条件的满意度[3]。

　　目标的隶属度函数的交集，可以表示为如下形式：

　　  ，

　　其中，分别表示解、目标和约束的隶属度函数，所以，含有L个目标（本文中L=3）和k个约束的多目标规划模型的解为：

　　其最优解为：

                       /* MERGEFORMAT        /* MERGEFORMAT

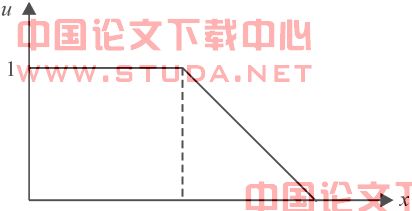
                    /* MERGEFORMAT  的隶属度函数图      

　　相应的目标函数隶属度函数的数学表达式为如下：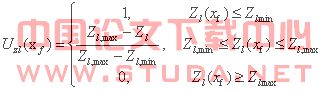     

　　在上述表达式中，是第L个目标函数的值，分别表示相应目标函数的偏离上限值和偏离下限值。

    所以可以将本文要求解的多目标线性规划转化为以下三个求最小值的多目标线性规划问题：

 /* MERGEFORMAT 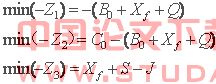 /* MERGEFORMAT

　　约束条件不变,依然为：

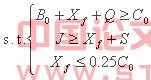
　　采用Zimmemann求解方 ，每次选择一个目标函数在所有的约束条件在分别求出最大值和最小值；用LINGO软件可求下列结果：

    为了求得符合以上三个目标的最优解，我们引入变量，，且使目标，由上述可知的值越大，满意度越大，方案的可行性越高。因此，本文中的多目标线性规划模型转化为如下容易求解的单目标线性规划模型：

　　通过某A区一类高校的各项统计数据，带入本篇的模型，得出A区学费 元，满意度 =0.72；将某B区的一类高校的各项统计数据，带入模型，得出B区学费 元， =0.69。

　　通过对以上的结果分析得出，上述两所高校处于不相同的两个地区，但是同属于一种档次的学校，两者的学费存在差异。由此，我们可以考虑高等，针对不同的地区、不同的专业采取不同的收费，实现教育的均衡发展。同时，这种学费标准与实际能够较好的吻合，且在上面的约束下保证了其合理与公平。同时可以看到，它们的满意度 都在较高的水平，可以使得社会各方都会很满意。

附录

%求解的lingo源代码（部分）

Model：

DATA:

C=14770;

R=28100;

B=8680;

J=9421.61;

S=5021;

Q=8260;

ENDDATA

MIN=-B-X-Q;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

Model：

DATA:

C=14770;

R=28100;

B=8680;

S=5021;

J=9421.61;

Q=8260;

ENDDATA

MAX=-B-X-Q;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

Model：

DATA:

C=14770;

R=28100;

B=8680;

S=5021;

J=9421.61;

Q=8260;

ENDDATA

MAX=-B-X-Q+C;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

Model：

DATA:

C=14770;

R=28100;

B=8680;

S=5021;

J=9421.61;

Q=8260;

ENDDATA

MIN=-B-X-Q+C;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

Model：

DATA:

C=14770;

R=28100;

B=8680;

S=5021;

Q=8260;

J=9421.61;

ENDDATA

MAX=X-S-J;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

Model：

DATA:

C=14770;

R=28100;

B=8680;

S=5021;

J=9421.61;

Q=8260;

ENDDATA

MIN=X-S-J;

R+X+Q>=C;

J>=X+S;

X<=0.25C;

DATA:    求出指定样本的学费

C=14770;

B=8680;

J=9421.61;

S=5021;

Q=8260;

a=-16940;

g=-20632.5;

h=-2170;

d=-5862.5;

e=-4400.61;

f=-8093.11;

ENDDATA

MAX = y;

(B+X+Q)>=C;

J>=X+S;

X<=0.25*C;

X>0;

(a-g)*y-0.1*(B+X+Q)<=a;   

(h-d)*y-(B+X+Q)+C<=h;

(e-f)*y+X+S-J<=e;

B+X+Q>=C;

J>=X+S;

X<=0.25*C;

y>0;

[1]张珍辉，彭尚平.高等教育多元化收费价格模型的构建[J]. 四川：西部科技

[2]戴罗仙，伍海泉.高等教育生均成本：界定、测算与运用[J].北京：教育与经济，2005

[3]周杰、牟小莉.多产品供应商选择的模糊多目标整数规划模型[M].北京：工程