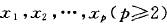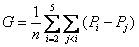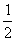多变才能多虑

       教学中适当的一题多变，可以激发学生去发现和去创造的强烈欲望，加深学生对所学知识的深刻理解，训练学生对数学思想和数学方法的娴熟运用，锻炼学生思维的广阔性、深刻性、灵活性和独创性，从而培养学生的思维品质，发展学生的创造性思维。下面结合本人的教学实践，谈谈我在教学中诱发一题多变的几种做法。
        一、启发 诱发一题多解
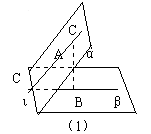
        教学中适当的一题多解,可以激发学生去发现和创造的强烈欲望,加深学生对所学知识的深刻理解,训练学生对数学思想和方法的娴熟运用,锻炼学生思维的广阔性和深刻性、灵活性和独创性,从而培养学生的思维品质,发展学生的创造性思维。比如,在教学中举个这样一道例题,如在梯形ABCD中，AB∥CD,∠A=90°,AB=2,BC=3,CD=1，E是AD中点.求证：CE⊥BE．  
        对于这道题目，我不是简单地就题论题，而是对其证法与学生进行了充分的探究。（下面是学生探究得到的几种证法）
        证法一：作CE⊥AB,在Rt△CBF中,由勾股定理易得：CF= ,又E是AD的中点,故DE=AE= ,分别在Rt△CDE和Rt△BEA中,由勾股定理易得： =3， =6，在Rt△CBE中，由勾股定理的逆定理可得: △CEB是Rt△，即CE⊥BE得证.
        证法二：分别延长CE、BA交于点F，易得△CDE≌△FEF，则CE=FE，AF=1，又AB=2，所以BF=3，又因为BC=3，所以BC=BF，在△BFC中，由三线合一定理得：CE⊥BE．
        证法三：取CB的中点F，连结EF，则EF是梯形CDAB的中位线，易得EF=2，则EF=CF=BF,则∠CEF=∠FCE, ∠FEB=∠FBE,在△CEB中，由三角形内角和定理易得∠CFB=90°，即CE⊥BE。
        通过对本题多种证法的探究，不仅唤起学生对已有知识和经验的回忆，沟通新旧知识之间的联系，而且培养了学生善于从不同角度思考问题的习惯，学生的自主意识和积极性得到了充分的发挥，收到了良好的教学效果。
        二、一题多变，挖掘习题涵量
        1．变换题设或结论。即通过对习题的题设或结论进行变换，而对同一个问题从多个角度来研究。这种训练可以增强学生解题的应变能力，培养思维的广阔性和深刻性，从而培养创新思维的品质。
        比如，同样对上述问题，我还对该题进行了多种角度的变式讨论，开阔了学生的眼界，活跃了学生的思维。
        变换1：在梯形ABCD中，AB∥CD，BC=AB+CD，E是AD中点。求证：CE⊥BE．  
        变换2：在梯形ABCD中，AB∥CD，CE⊥BE．, E是AD中点． 求证： BC=AB+CD。
        变换3：在梯形ABCD中，AB∥CD，BC=AB+CD, CE⊥BE．判断E是AD中点吗？为什么？
        变换4：在梯形ABCD中，AB∥CD，BC=AB+CD， E是AD中点．求证： 
        2．变换题型
        即将原题重新包装成新的题型，改变单调的习题模式，从而训练学生解各种题型的综合能力，培养学生思维的适应性和灵活性，有助于学生创新思维品质的养成。 

        例如：已知△ADE中,∠DAE=120°，B、C分别是DE上两点,且△ABC是等边三角形, 求证；