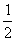构造函数法在解题中的应用

        解析：本题主要考查了恒成立问题的基本解法及分类讨论思想，属于难题。
        已知f（x）为增函数且m≠0，
        若m>0，由复合函数的单调性可知 和 均为增函数，此时不符合题意。
        M<0，时有 因为 在 上的最小值为2，所以1+ 即 >1,解得m<-1。
        点评：本题是较为典型的恒成立问题，解决恒成立问题通常可以利用分离变量。
        例7：已知函数 ，是否存在实数 ，使得 的图象与 的图象有且只有三个不同的交点，若存在，求出 的取值范围，若不存在，说明理由。
        解：函数 的图象与 的图象有且只有三个不同的交点，即构造函数。的图象与 轴的正半轴有且只有三个不同的交点。当 时， 是增函数； 当 时， 是减函数；当 时， 是增函数； 当 或 时， 当 充分接近0时， 当 充分大时， 要使 的图象与 轴正半轴有三个不同的交点，必须且只须所以存在   ，使得函数 与 的图象有且只有三个不同的交点。
        四、构造函数解决几何问题
        在几何问题中, 我们往往会遇到求夹角的最值和求线段的最短(长)距离等问题，如果仅从几何方面去思考,往往使问题难以解决, 倘若能够灵活地运用构造函数方法, 从而使几何问题“柳暗花明”。
        例8（2010福建文科数学）：若点O和点F分别为椭圆 的中心和左焦点，点P为椭圆上的任意一点，则 的最大值为          
        A．2    B．3 C．6   D．8
        解析：由题意，F（-1，0），设点P ，则有 ,解得 ，因为 ， ，所以=  = ，此二次函数对应的抛物线的对称轴为 ，因为 ，所以当 时， 取得最大值 ，选C。
        从以上几例的解答中，我们已初步看到了函数思想的应用，函数思想的应用想当广泛，但这些方面都涉及到最基础知识，只要在学习中扎扎实实地掌握基础知识，学会全面地分析问题，并注意在解题中不断总结经验，就一定会真正掌握运用函数思想解题的思路和方法，从而收到事半功倍的效果。 
参考文献： 
[1]郭静莉.构造函数法在高等数学解题中的应用[J].赤峰学院学报(科学教育版)，2011(2).
[2]李智. 浅谈高等数学解题中构造函数法的应用[J].科技资讯，2008(16).
Abstract: Functional idea is an organic ingredient in mathematics idea and it is widely used in mathematics problem-solving. This paper analyzes the application of constructed function approach in inequality, progression, the existence of the solution and constant established.
Key words: functional idea; constructed function; inequality; equation; application