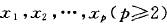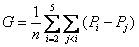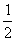测度论中的存在性及唯一性
关键词:λ-系;σ-代数;概率测度;延拓
论文摘要: 测度论是数学的一个重要分支,在概率统计、随机过程、微分方程、微分几何中有广泛应用。测度理论是实变函数论的基础。集类知识与单调类定理是测度论中的基础,特别是单调类定理.这个定理是一个很要紧的定理.在后面证明测度唯一性定理,乘积测度存在定理等重要的定理中有涉及。在严加安老师的《测度论讲义》上这个定理有两个版本,目前该书是对单调类方法应用的最多的。有一些看起来很难的问题,也许用这个定理会相当简单.将定义在一个λ族上的概率测度延拓为包含该λ族的一个σ上的概率测度,在许多重要场合,特别是在学中有着十分重要的意义.关于这种延拓的存在性、唯一性等,给测度论提出了一系列新的理论课题,本文试图对λ族上概率测度的延拓问题作一些初步探讨.

族性质的引申:设![]() 为
为![]() 上的一族非负有界函数,我们用
上的一族非负有界函数,我们用![]() 表示非负有界
表示非负有界![]() 可测函数全体,则下列二断言等价:
可测函数全体,则下列二断言等价:


第二步:令![]() 2=
2=![]()
![]() 2
2![]() (*)
(*)
则(a)![]() 2 (b)
2 (b)![]() 2是
2是![]() 族 (证法与上面(a)(b)类似略)
族 (证法与上面(a)(b)类似略)
从而![]() 2且
2且![]() 2
2![]()
![]() 2
2

![]() 则
则![]()
![]()
![]()
![]()
![]()
![]() F是
F是 ![]() 类从而F使
类从而F使![]() 代数
代数
第四步:![]() 对有限个的下端运算封闭:
对有限个的下端运算封闭:
![]()
![]()
Proof:不妨设![]()
![]() (
(![]()
![]() 中元素均非负有界)
中元素均非负有界)
故![]()
往证:(a)![]() (b)
(b)![]()
Proof:(a)依第二步![]() ,
,![]()
![]()
![]()
![]()
![]()

第五步:![]() 要证
要证![]() 从而
从而![]()
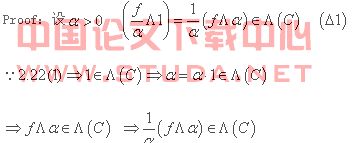
由 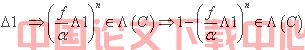
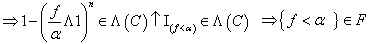
![]() 为
为![]() 可测,对
可测,对![]()
第六步:往证![]()
设![]() ,则
,则![]() 有界且
有界且![]()
![]()
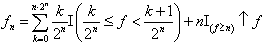
依![]() 的定义及第五步:
的定义及第五步: