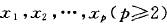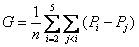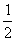浅谈恒成立问题的解题方法

        函数与不等式既是知识的结合，又是数学思想和方法的交汇处，因此成为高考的热点。恒成立问题就是其中一种比较常见的题型。恒成立问题在解法上是灵活多样的，其某些解法及解题思想，对解决其它数学问题也有一定的指导性作用。本文旨在通过对具体问题的解析，来帮助学生加强对这一类问题的掌握。
        一、变换主元
        例1、设不等式mx2-2x+1-m<0对于满足|m|≤2的一切实数m的值都成立，求x的取值范围。
        分析：若本题改为“不等式mx2-2x+1-m<0对于任意的实数x恒成立，求m的取值范围”，则问题可化归为文[1]中的例2进行求解。但对于本题学生则难于下手，这是因为学生的思维定势，将x看成自变量，m看成是参数，求解确实困难。但如果我们能够换位思考，变换主元，将m看成自变量，x看成是参数，将原不等式变形为（x2-1）m+1-2x<0，这样就可以将问题转化为关于m的一元一次不等式来求解，则问题可迎刃而解。
解：原不等式转化为（x2-1）m+1-2x<0，记f（m）=（x2-1）m+（1-2x），其中-2≤m≤2。
        根据题意得
        说明：本题将m视为主变量，则f（m）的图像是一条线段，即f（m）为一次函数，可利用一次函数的单调性求解。
        二、巧用等号
        例2、已知二次函数f（x）=ax2+bx+c的图像过点（-1，０），问是否存在常数a、b、c使得对于任意的x，不等式x≤f（x）≤（1+x2）恒成立？
分析（一）：本题也为恒成立问题，需将不等式x≤f（x）≤　（1+x2）看成“对于任意的x，x≤f（x）与f（x）≤（1+x2）同时恒成立”，故需两次利用恒成立思想来求解。
        解：由题意知：对于任意的x，x-f（x）≤0与f（x）-　（1+x2）≤0恒成立，
即ax2+（b-1）x+c≥0……（1）与x2+bx+c-　≤0……（２）恒成立。
        又函数f（x）=ax2+bx+c的图像过点（-1，0），故a-b+c=0，即a+c=b。
        所以a=c，2（a+c）-1=0。
        所以存在常数a=c=　、b=　满足题意。 
        分析（二）：如果我们能观察不等式x≤f（x）≤　（1+x2） 的特征，巧妙利用其中的两个等号，则问题将会变得简单得多。