寓问题探究于课堂教学之中
内容摘要:
为落实《数学新课程标准》所提出的教改目标,采用情景教学模式,本人所尝试研究的一种教学方法。
一、精心设计探究问题的情景,激励学生的探索意识。
二、在例题教学中恰当引导,教会学生探索的方法。
三、留给学生探索的时空。
四、自己的一点体会。
关 键 词:
情景设计、问题探索、课堂教学
作为新课程改革的有机组成部分,课堂教学改革是不可缺少的重要一环,改革课堂教学技术要用新课程的理念指导课堂教学设计。转变学生消极被动的学习方式,培养学生的创新精神和实践能力。数学课堂设计,即是要以《数学新课程标准》界定好的课程理念为指导,逐步实现新课程标准设定的各项目标,让学生在学会数学知识的同时,学会探究,学会合作,学会应用,学到创新。
认知心认为:学生只有参与实践,参与问题探究,才能建立起自己的认知结构,才能灵活地运用所学知识解决实际问题,才能有发现,有创新:数学知识、数学思想方法必须由学生在实际的数学活动中理解和掌握,而不是单纯地依赖教师的讲解,不是以机械模仿的方式进行学习。为此,笔者在课堂教学中,积极创设问题情境,鼓励学生主动地参与问题的探究过程,教会形式探究的方法,留给形式自主探究的时间,设计具有探究性的课堂练习及课后作业,培养学生探究问题的能力。
一、精心设计探究问题的情景,激励学生探究的意识。
培养和提高数学思维能力,是数学教育的基本目标之一。学生在学习和运用数学解决问题时,不断地经历归纳类比,空间想象,抽象概括,符号表示,运送求解,数据处理。演绎证明,反思与建构等思维过程,对客观事物中所蕴涵的数学模式进行思考判断,但这一思维过程离不开直观感觉,观察发现,而用实际的例子(即适度的形式化)来加以表达,学生更容易接受,这即是数学课堂设计应遵循的情境性原则,美国心理学家布鲁纳·黑杰斯认为:“在教学过程中,学生不是被动的消极的知识接收者,而是积极的主动的知识探究者;教师的作用是要形成一种使学生能够独立探究的情景,激发学生发现问题,探究知识的强烈欲望和兴趣,使课堂变为探究性活动的课堂。
比如,“无穷递缩等比数列求和”是在学生学习了数列及数列极限等知识基础上提出来的,它与数列、方程、函数和极限等知识有内在联系,能与实际生产和生活中的问题相结合。但是学生对无穷数列各项的和有限到无限的思想方法,以及用极限的思想方法去解决实际问题还缺少思想基础,为此,笔者在教学过程中设计情景,通过实际问题,以引起学生性感体验,引导学生学会构建,最终到达教学目标。
1、提出问题——激发兴趣
问题 1:如果不停地往一只空箱子内放东西,箱子会满吗?为什么?
这一问题表面上是一个游戏,事实上,它隐含着无穷数列各项和的知识,有一定的趣味和魅力,能引起学生的思考。不同层次的学生都 有发言权,也不乏味,有能力点,个性和创新精神培养点,学生从实际背景出发;通过动脑思考,动手操作,动口说明,能经历从抽象表示到符号变换和检验应用全过程,能培养学生的数学建模能力。
2、自主探索——感知问题
教师先用提示学生用教学眼光去看上述问题,即将上述问题转化成数学模型。然后让学生开展研究。
3、合作交流——形成共识
(1)问题一的讨论。
S1: 箱子即使很大也会满,因为,设第一次放入量为A1,第二次放入量A2…,则A1+A2+A3…可能很大。
S2: 箱子即使很小也不会满,因为,第一次放入量为A1,第二次放入量为A2,…,则A1+A2+A3+…可能很小。
(2)有关问题1的例子
问题2;你能尽可能地举出箱子不会满的例子吗?
S3:把一支粉笔的一半放入箱子中,剩下的粉笔的一半即原粉笔的 再放入箱子中。如此下去……,放入箱子中的粉笔只有一支,不会满,其数学模型是:
a+ a+ a+…=a (a是粉笔的长度)
S4:把一杯水的 倒入容器中,剩下的 再倒入容器中,如此下去,…,倒入容器中的水只有一杯,不会满,其数学模型是:
b+ b+ b+…=b (b是一杯水)
(3):无穷递缩等比数列的定义。
问题3:你能否将S3Z这类问题一般化?若设第一次放入空箱子中的量为a1,第二次放入空箱子的量为a2,…,第n次放入空箱子的量为an,…,数列{an}有何特点?
S5:数列是等比数列,也是递减数列,且是无穷的。接着再让学生自主研究无穷递缩等比数列的定义,并判定数列{an}是不是无穷 等比数列?同时,进一步思考无穷递缩等比数列是否一定是递减数列?并举例说明,加深对概念的理解。
(4):Sn与S的关系
问题4:当|q|<1,an=a1qn-1,可以证明,当n→∞时,an→0(学生课后研究证明方法)请学生思考:若设数列{an}前项和为Sn,所有项的和为S,运用极限的思想,你能否发现Sn与S的关系?
讨论结果: S= Sn
(5)求无穷递缩等比数列的和。
问题5:怎样求无穷递缩等比数列{an}的和?
讨论结果:
Sn=a1+a2+…an=
因为当|q|<1时, =
T : 好!我们通过自主探索与合作交流得出了无穷递缩等比数列的求和公式 S= (|q|<1)
问题6:公式的应用(略)
通过应用交流使学生加深对公式的认识,体 了教学模型化思想,让学生在交往学习数学。
4、反思—共同创新
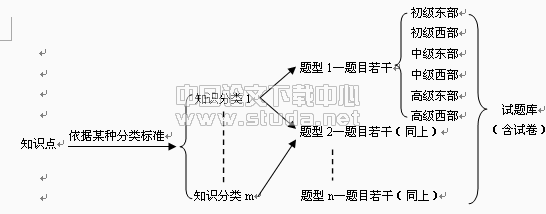
本课我们运用情景化,理想化抽象化等数学方法,将游戏问题 转化为数学模型→无穷递缩等比数列的和,为了概括所学内容的逻辑结构 提炼思想观点,使学习形成新 的知识结构,引导学习创新,可将本课研究过程和方法概括如下:
在本课中,学习积极参与问题的探究,在热情高涨的氛围下笔者顺利地完成了教学任务,通过课堂和课后练习,效果很好,事实上,只要教师做有心人,将课本的知识点精心设计,挖掘其生活原型,在课堂教学中,教师努力引导学生运用正确的学习方式,力求体现教学学习是“经验、活动、思考和再创造”的特点,使课堂处于不断的动态变化中,从而培养学生探究问题的能力。
二:在例题教学中恰当引导,教会学生探究问题的方法。
的进步是以方法的进步为推动力的,同样课堂效率的提高也离不开科学的教学方法和学习方法,笔者在教学过程中,时时注意学习方法和解题策略的渗透,注重学生创新能力和科学探究能力的培养,开发学生的潜能,彻底改变学生被动学习的方式,为课堂教学注入新的活力。
例如 ,在学习了用导数求函数的极值,最后,为了加深学生对求函数极值,最值方法的理解,可设计如下问题让学生探究 ]
设 f(x)+3x2+ -20,x∈(0,+∞),求实数a的范围,使对任意 x (0,+ ),都有不等式f(x) 0恒成立。
几分钟过后,有的同学提出,只要求出x3(20-3x2)的最大值即可,为什么?怎样求呢?犹如一石激起千层浪,立即引起学生的探究兴趣,很快许多学生“天门”大开,找出用导数求解的方法:
由 f(x)=3x2+ -20≥0得,a≥x3(20-3x2)
令g(x)=x3(20-3x2) 只要a不小于函数g( )在(0,+ )上的最大值即可,由 =60x2-15x4=0得x=2
因为g(x)在(0,+ )上只要一个极值且x + 时, g(x) - .所以当x=2时 g(a)取最大值,既gmax=g(2)=64 所以当 a 64时。 f(x) 恒成立。
这样将问题直接呈现在学生面前,让学生通过相互讨论探究解决问题的方案,尽管会花费较多的时间。但这样做是值得的。只要这样学生才能从对教师的依赖中走出来,养成自己探究学习问题的良好习惯。
三、留给学生探究问题的时空
前苏联家达尼洛夫说过:“教师对学生讲得越多,从而留给学生独立地获取知识,独立思考和进行活动提供的机会就越少,教学过程的活力和效果就越近。”在课堂教学中,教师把问题提出后,应让学生有较宽余的思考和探究问题的时间和空间。让他们有更多的体验,感悟,探究,实践的机会。在新课讲解,点到直线的距离公式时,笔者按特殊到一般的原则设计教案,引导学生去探究,设计如下“先让学生求点P(1,1)到直线 x+2y+1=0的距离,并让学生思考有几种求法,点评后再将问题一般化 ,既设P(x0,y0)为直线 Ax+By+C=0外的一点,求P到 的距离,学生在求上面具体点到直线狐狸的基础上。很容易找到解决问题的方案,这样留给学生自己探究的时空。让每个学生都经历“体验、探究”的过程,让每个学生根据自己的体验,用自己的思维方式自由地开放地去探究、发现、创造,使学生探究问题落到实处。
四、一点体会。
通过教学实践,笔者深刻体会到,以往教室高容量,高密度,快节奏,使学生无暇思考,只会依葫芦画瓢,眼里有思路,心里没有思路,不会在自己的头脑中创造出思路,只能永远重复他人。现在我们打破以往在课堂教学中,让每个学生通过问题探究活动,构建自己对问题的理解和解答。并在与 同学和教师交流的基础之上,悟出对问题以及相关数学知识方法更为深刻的理解,增强了学生学习数学的兴趣和信心,使学生不正确的学习方式得到根本改变,有效地促进了学生探究能力的。
:
[1]周春荔、刘兴化 数学研究性学习及其特点 中学数学 2004年第1期
[2]周小山 教师教学究竟靠什么—谈新课程的教学观 北京大学出版社
[3]沈文选 数学教师专业化与教育数学研究 中学数学 2004年第2期
[4]徐伏儿 情景中活动、活动中体验、体验中领悟 中学数学教与学 2004年第2期
[5]吴中魁 有条不紊、有的放矢 中学理科 2004年第1期
[6]潘伟东 几种数学思想方法在解题中的应用 数理化学习 2004年第7期