小学生视图能力的测试分析及其对几何课程设置的启示
摘要:小学几何课程如何培养学生的空间观念是备受关注的问题。利用“视图测试卷”,对2~6年级的405名小学生视图能力和水平进行测试,结果表明,对于2~4年级学习或接触过相关内容的小学生,视图的能力和水平不存在年级间显著差异,学习或接触过相关内容的低年级小学生对视图的理解水平大都接近甚至高于未学习过相关内容的高年级小学生;小学生在视图认识上不存在显著的性别差异;等等。此研究结果对小学数学课程的设置和教学提供了不少启示。
关键词:空间能力;小学数学;几何课程;视图
Abstract:How to develop student’s spatial sense by geometry curriculum is drawing more and more attention. We have designed the “Test of Orthogonal View” to make a survey on 405 pupils from grade 2 to 6 to test their ability and standards of orthogonal view. It is found that pupils from grade 2 to 4 who have learned or contacted orthogonal view don’t have instinct cognition differences between the grades. Pupils of lower grades who have learned or contacted orthogonal view performed as good as or even better than higher grade pupils who haven’t learned or contacted orthogonal view. Pupils don’t have instinct sex differences in cognition of orthogonal view. Based on the findings of this study, some suggestions for primary school teachers and curriculum setup have been made.
Key words: space ability; primary mathematics; geometry ; orthogonal view
一、问题的提出
几何课程对学生空间能力的重要性已是不争的事实,然而,如何设置几何课程以发展学生的空间能力的研究却还有大量的工作要做。国际数学委员会(ICMI)的研究报告(1998)指出, [1]几何课程不能局限于平面部分,平面几何也不能局限于“微观空间”(指练习本和书本)。相反,特别在低年级,几何教学的起点必须是对我们所生活的现实三维空间的仔细观察,而且这种对三维空间的注意必须持续到高年级,并把焦点放在二维和三维空间的关系上,如我们眼中的物体与纸上的图形及机上的图形之间的关系。在课程中,除了度量性质外,还应该包括平面的仿射性质以及平面到平面的平行投影,当然,还可以考虑中心投影。
因此,注重联系“现实三维空间”,关注“二维和三维空间的关系”,成了一些国家几何课程中发展学生空间能力的出发点和着眼点。如果再考虑“投影”这一因素,那么很自然地想到“视图”。然而,可能对于大多数处于小学阶段的学生,与其对正投影概念进行严格定义和描述,不如用他们所具有的几何直观(视觉直观)的能力去感知三维世界,从而理解不同位置、不同角度观察到的物体形状会不同及为什么不同,识别和表示这些不同的形状,了解与这些形状相对的位置、角度,等等。因此,如果能够把这部分既与“三视图”有密切联系而又不同于其在几何上严格的定义且融合了更多现实空间成分的内容,以恰当的方式体现在小学的几何课程中,必将对学生的空间观念的培养起到积极的作用。这是目前数学课程建设与开发急需解决的问题。
心上虽然已有一些关于“视觉透视”等问题的研究,但大多是对特定群体针对个别具体问题的研究,而对不同年龄阶段的小学生关于“视图”内容的较为全面的认识水平的研究却没有。在数学教育领域,只是凭借经验以发展学生的视觉直观及空间观念为目的制定了一些课程和教学计划,同样对学生是如何认识的似乎都没有涉及。随着《全日制义务教育数学课程标准(实验稿)》(下称《标准》)的颁布及推行,当前我国的小学课程中也安排了相应的教学内容。 [2]因此,本研究针对一部分小学生进行了测试,旨在寻求不同年龄、不同学校类型、对视图初步内容有着不同熟悉程度的小学生对视图初步有着怎样的认识,以及男女学生在性别上是否存在显著的认识差异,希望测试与分析的结果能对小学阶段的几何课程中相关内容的设计提供实验的基础。
二、研究方法
(一)被试的选取
本研究在北京市的一所城区小学(A)和一所郊区小学(B)中选取2~6年级的学生作为被试,在每个学校中,从各个年级随机抽取一个自然教学班,共405人。
表1 两所学校被试学生的一般信息
二年级 三年级 四年级 五年级 六年级 每个学校的学生总数/男生数 A 35 36 45 45 38 199/104 B 41 46 42 41 36 206/115
需要说明的是,A校的2~4年级的学生使用的是根据《标准》编写的北京师范大学出版社出版的教材,但5~6年级学生用的则是根据2000年的《小学数学教学大纲》编写的北京教育出版社出版的教材,没有学习或接触过视图方面的知识;B校2~6年级使用的也是根据2000年的《小学数学教学大纲》编写的北京教育出版社出版的教材,但据校方介绍,除了6年级,该校在2~5年级的教学中均讲了一些“从不同方向观察物体”的内容。
(二)研究方法与工具
我们设计了“视图测试卷”,采用个人独立答卷的方式进行。试题的设计主要根据曹才翰(1990)提出的空间观念的五个要求等, [3]分析了一些相关的研究及课程设置,从三个维度、三个方面设置问题来评价学生对视图的认识。三个维度分别为识图、读图和画图,对三个维度各有所侧重;三个方面是指从生活到生活、从生活到数学及从数学到数学。(例题见附录)
识图这类题目要求学生对呈现的空间或几何体识别它在不同方向或角度下的不同的视图;画图这类题目要求学生对呈现的空间或几何体画出指定方向或角度的视图;而读图这类题目则要求根据某个(些)方向或角度的视图建立起整个空间或几何体的结构。
对于三个方面,从生活到生活的题目要求学生从所处的生活空间出发,用“生活的”眼光来分析生活中的事物及它们之间的关系,认识到不同的视点对应着不同的视图。从生活到数学的题目要求学生从所处的生活空间出发,用“数学的”眼光分析生活中可以被模型化的事物,有一定的抽象。从数学到数学的题目要求学生从数学的几何图形出发,通过想象按要求抽象地分析图形的关系和特征,实现二维与三维图形间的转换。
题目设计过程中,征询了心理学专家和数学教育专家的意见,还参考了国际测试(如TIMSS)和其他一些研究中的试题,并抽取北京城区某小学的2年级20人、5年级30人共50名学生进行试测,最后确定了用于测试的29道题目,其中识图部分14道题,读图部分8道题,画图部分7道题。
正式施测是在2005年11月至12月间,由笔者亲自参与完成。整个测试卷的总分为55分。本测验的数据采用SPSS13.0统计软件包进行管理分析。
三、测试结果及分析
(一)信度分析
测试完毕,采用Cronbach’s Alpha系数法测得各部分(识图、读图和画图)及整个测验的信度,见表2。
表2 各维度和总测试的Cronbach’s Alpha系数
识图 读图 画图 总测试 Cronbach’sAlpha0 0.693 0.634 0.805 0.853
学者DeVellis(1991)认为,一份信度系数好的量表或问卷,最好在0.80以上,0.70至0.80之间还算是可以接受的范围;分量表最好在0.70以上,0.60至0.70之间可以接受。因此,本测验是可以接受的。
(二)测试结果及分析
1.年级间总体趋势分析
由于两个学校的2~4年级均学习或接触过视图初步内容,首先考察这三个年级视图认识水平的总体发展趋势,其总平均分的趋势如图1。
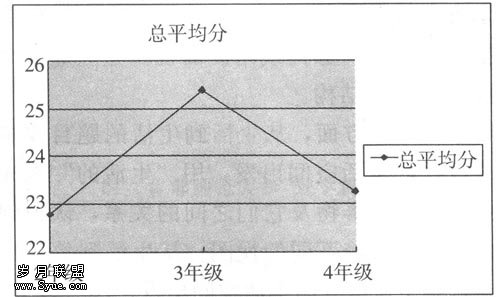
图1 2~4年级总平均分趋势图
从图形中能够看出,3年级成绩略好一些,但方差分析的结果表明,三个年级间不存在显著差异。因此我们可以认为从总体上来讲,这三个年级之间在视图部分的认知水平差异不大。
进一步对2~6年级总体成绩以及三个维度的成绩进行方差分析,我们发现,均存在显著差异。具体分析年级间出现的显著差异,其结果表明:在识图这个维度上,2、4、6年级分别与5年级存在显著差异,并且2年级的成绩好于4、6年级;在画图这个维度上,2、4、6年级分别与5年级存在显著差异;在读图这个维度上,2、4年级分别与5年级存在显著差异,6年级的成绩略好于2、3、4年级。除此之外,其他年级间不存在显著差异。
2.各学校学生年级间和性别差异分析
两个学校的总情况如图2,从图中我们可以直观地发现,除5年级外,A校的各年级好于B校的各年级,而B校的5年级是接触过视图内容的。
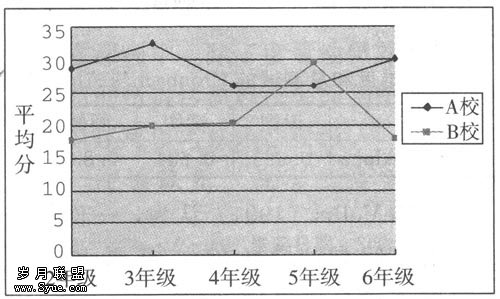
图2 两所学校2~6年级总平均分趋势图
为了进一步全面地考察小学生对视图初步认识在年级和性别上的差异,针对两所学校的不同情况,我们又以各个学校为单位,就测试总分进行了年级间方差分析和相邻年级间差异检验,也对性别的差异进行了分析。
A校和B校的各年级总成绩的方差分析结果都表明,该校的被试学生在理解上存在显著的年级差异;性别差异分析表明,男女学生之间差异不显著。
对两个学校分别做的年级间差异检验结果表明,两个学校中学过或接触过视图知识的年级对视图的认识达到比较高的水平,而对于没有学过的年级,则表现出来的水平比较一般。如A校,其2~4年级是学过的,与高年级相比,水平较高,尤其是3年级的成绩比较突出,但与2年级不存在显著差异,而与4、5年级间存在显著的差异,4~6年级之间保持相对稳定的状态,但都与2年级不存在显著差异,也即与2年级水平差不多;对于B校,2~5年级均接触过视图的知识,但学生的认识在2~4年级稳定发展,4~5年级是个快速发展的阶段且在5年级达到最高水平,出现与其他年级间的显著差异,但在6年级则又回复至与2~4年级相近的水平。
四、结论
(一)小学生对视图认识的性别差异
数学能力的性别差异是数学心研究领域内的基本课题,国际上对此已有几十年的研究。而空间能力上的性别差异(主要还是分为空间定向和空间想象能力这两类)很早就被人们所发现,并吸引了许多研究人员的注意。但对空间能力是否真的存在差异、差异的大小、过程和产生原因却不能形成一致意见。不同的研究选择了空间能力的不同方面,得出了不同的结果,对于不同年龄段的被试,结果也不相同。 [4]西方学者对儿童或小学生所做的研究都表明男孩在空间能力上占一定优势。但是国内学者的一些研究结果与西方学者的结果有一定出入。许燕和张厚粲对2、4、6年级的小学生空间能力的研究结果表明, [5]在各年龄组均未显示出很大的性别差异,其变异数均未达到显著性水平;2、4年级的男生占有一些优势,但到了6年级则发生优势“翻转”现象,表现出女生平均分略高于男生。从性别差异的发展倾向上来看,男生在空间能力上的优势表现为随年龄增长而缩小并消失的特点,这说明男生在空间能力上的优势并不是恒定的。这可能说明儿童具有与西方儿童不同的空间能力性别差异表现特征。
本研究在这一部分的结果是,小学生在对视图的认识上不存在显著的性别差异。作为数学课程的一部分,且是与发展空间能力相联系的课程内容,这一结果同样是与已有的研究结果相符合的:中国儿童在数学或空间能力上可能不存在显著差异,至少是在小学期间。 [6]
(二)小学生对视图的认识特点
本测试结果说明, 总体上说2~4年级学习或接触过相关内容的小学生对这部分内容的认识是平稳发展,虽然在4年级稍有回落,但不存在年级间显著差异。而对2~5年级情况一致的B校的分析表明,4~5年级是学生认识发展的一个关键时期,并在5年级达到了与其他年级有着显著差异的水平。在访谈中,B校的5年级学生告诉笔者,他们接触过这种类型的课程内容,而且教师还进行过多媒体教学──他们曾通过一些多媒体软件学习过相关的知识,如利用机呈现出一个三维的实物,要求他们选择从不同角度看到的二维图形;而在A校,4年级教师则反映他们对这部分内容接触不多,识图的多些,基本上是课程之内的。
五、启示
通过对本测试结果的分析,我们从课程和教学的角度作了如下几个方面的思考。
无论是对两所小学进行的共同分析还是对他们各自的分析,都表明2年级学生的总体平均成绩以及在识图、读图和画图三个维度的成绩都与其他年级的成绩没有显著差异(5年级除外),并且3、4年级的稳步发展说明了学生对视图内容理解掌握的稳定性。这说明视图的一些基本知识在小学第一学段就能够被学生较好地接受和掌握,因此从第一学段的开始就可以安排一些适当的视图内容供学生学习。
从6年级的总体表现和在三个维度的表现看出,6年级在识图和画图等维度均不如其他年级,虽然其中可能存在学习态度上的问题,比如对学习的兴趣和对测试卷回答的厌倦等因素,但从访谈的情况看出,6年级学生对某些问题的想象的意识和水平确实与2、3年级相当甚至低于低年级的学生。这从某种程度上说明在小学低年级段引入视图的内容,对学生空间观念的发展是有利的。
分析测试结果还能发现,不同年龄段的小学生在三个不同维度上的认知发展特点也有不同。6年级在识图和画图方面不如其他年级,但在读图方面表现最好。究其原因,读图对学生的要求不仅仅是直观的想象,还要有一定的空间推理能力和逻辑思维能力,而这些都要求学生具有一定的思维水平,无论是在皮亚杰(Piaget)的思维发展阶段理论 [7]中还是范希尔(Van Hieles)的几何思维水平 [8]中,都是属于较高的思维层次和水平了,因此在测验的结果中也就体现出了年龄的差异性。
这样就为我们的课程编制提出了一个问题:如何在小学的不同年龄段安排不同的视图内容,以适应学生的思维发展和空间能力发展的需要?
对五个年级小学生识图、读图和画图三个方面所作的方差分析检验的结果显示,识图以及简单的读图和画图内容适合在低年级安排,而且可尽量以“从生活到生活”的方式呈现,这不仅适合学生年龄特征的要求,也因为贴近生活而使学生的想象有了更多的观察基础,为他们创造出更广阔的观察想象空间。随着年级的增高,可以逐渐安排读图和画图的内容,将想象与空间推理和逻辑思维结合起来。
课程实施过程中教学方法和手段的运用,也是值得考虑的问题。如何为学生提供想象的空间,如何组织观察、想象、操作等环节,如何运用现代化的信息技术等都是教师在具体教学过程中针对不同的内容和学生需要考虑的问题。
在对学生的答卷进行分析的过程中,还引发我们思考了有关如何引入视图概念的问题。关于“视图”概念的引入,目前一些教材的做法是“从不同的方向看”,也就是“生活化”地去处理,我们问卷中的问题也是这样提出的,但我们发现一些学生却是用透视的方法画出看到的图形来表达他们对此的理解,应该说对于我们提出的问题,学生的理解是有道理的,这也暴露出“从不同的方向看”引入的视图在严谨性方面存在的问题。但是,对于小学生来讲,直接由正投影引入视图的概念未免过于形式化。因此,怎样引导学生理解“从不同的方向看”,进而从正投影的角度理解视图,是课程编制和教材开发需要深入思考的问题。
附录 例题
1.下图中的玩具房子可以看成是由右边的两个几何体组成的,请根据这些图形回答下面的问题。
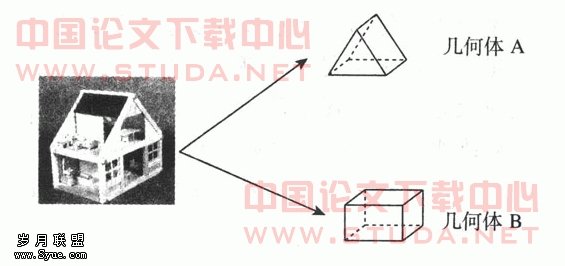
(1)从上面看几何体B所看到的图形是下面哪一个?在你认为正确的答案上打“√”。
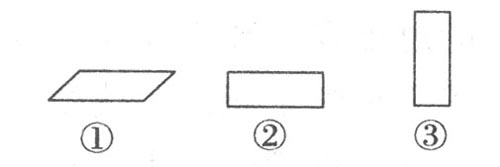
(2)你能画出从正面、上面和侧面看几何体A时所看到的图形吗?
2.有一个用小立方块搭建的几何体,从正面看是![]() ,从上面看是
,从上面看是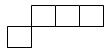 ,下面哪个立体图形符合,请在对的括号里打“√”。
,下面哪个立体图形符合,请在对的括号里打“√”。

:
[1]Perspectives on the Teaching of Geometry for the 21st Century—An ICMI Study(Volume 5). The Netherlands:Kluwer Academic Publishers,1998.
[2]中华人民共和国教育部.全日制义务教育数学课程标准(实验稿)[S].北京:北京师范大学出版社,2001.
[3]曹才翰.中学数学教学概论[M].北京:北京师范大学出版社,1990.
[4]钱红.空间能力性别差异研究进展[J].宁波大学学报(教育版),2002,(6):13—17.
[5]许燕,张厚粲.小学生空间能力及其发展倾向的性别差异研究[J].心理科学,2000,(2):160—164.
[6]张厚粲,王晓平.中国儿童认知能力的性别差异发展倾向:韦氏儿童智力量表结果分析[J].心理科学,1996,(2):65—70.
[7]Jean Piaget. The Child’s Conception of Space [M]. London: Routledge & K. Paul,1956.
[8]A J Bishop. International Handbook of Mathematics Education[M]. Netherlands :Kluwer Academic Publishers ,1996:161—204.