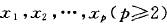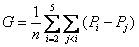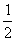费马点

而费尔马曾提出关于三角形的一个有趣问题：在三角形所在平面上，求一点，使该点到三角形三个顶点距离之和最小。即在ABC内求一点P,使 PA+PB+PC之值为最小,人们称这个点为“费马点”。
今天我们来探索费马点。首先将三角形分为两种情况:
①当三角形有一个内角大于或等于一百二十度的时候，则费马点就是这个内角的顶点。
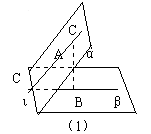
下面来验证这个结论: 对三角形内任意一点P,延长BA至C’使得AC=AC’，做∠C’AP’=∠CAP，并且使得AP’=AP, PC’=PC，即把三角形APC以A为中心做旋转变换(如图)。

则△APC≌△AP’C’（旋转的不变性）
∵∠BAC≥120°（已知）    
∴∠PAP’=180°-∠BAP-∠C’AP’（平角的意义）=180°-∠BAP-∠CAP（等量代换）=180°-∠BAC≤60°
∴等腰三角形PAP’中（已知AP’=AP），AP≥PP’（∠PAP’＜∠AP P’）
∴PA+PB+PC≥PP’+PB+ P’C’>BC’（两边之和大于第三边）=AB+AC（已知AC=AC’）
所以A是费马点。即之前的结论。
下面探讨第二种情况：
②如果三个内角都在120度以内，那么，费马点就是使得费马点与三角形三顶点的连线两两夹角为120度的点。
做△ABC内一点P，使得∠APC=∠BPC=∠CPA=120°，分别作PA,PB,PC的垂线，交于D,E,F三点（如图），再作一点P’，不与点P重合，连结P’A,P’B,P’C，过P’作P’H垂直EF于H。
 
∵∠APB=120°，∴∠PAB+∠PBA＝180°－120°=60°
且∠PAF=∠PBF=90°，∴∠F=180°－（90°+90°－60°）
同理可得：∠D=∠E=∠F=60°，即△DEF为等边三角形，设边长为d，面积为S。
则S= 1/2 d (PA+PB+PC)
∵P’H ≤ P’A
∴ 1/2×d×P’H×2S ≤1/2 ×d ×P’A×2S
又∵1/2×d×P’H=△EP’F  ∴ 2S△EP’F≤ d ×P’A×S
同理有：2S△DP’F≤d ×P’B×S ， 2S△EP’D≤d ×P’C×S
相加，得：2S(△EP’F+△DP’F+△EP’D)≤ d ×S (P’A+P’B+P’C)
又∵△EP’F+△DP’F+△EP’D=△EDF
2S×S ≤ d ×S (P’A+P’B+P’C) 两边同除以S，得：2S ≤ d  (P’A+P’B+P’C)
把S= 1/2 ×d (PA+PB+PC)代入上式可得：
PA+PB+PC≤P’A+P’B+P’C，当且仅当P,P’重合时取到等号。
所以P是费马点，即与上述结论相符合。
经过上述的推导，我们即得出了三角形中费马点的找法：
当三角形有一个内角大于或等于一百二十度的时候，费马点就是这个内角的顶点；如果三个内角都在120度以内，那么，费马点就是使得费马点与三角形三顶点的连线两两夹角为120度的点。
初二㈢班   林贤昊
费马（Pierre de Fermat,1601—1665）是法国数学家、物家。费马一生从未受过专门的数学，数学研究也不过是业余之爱好。然而，在17世纪的法国还找不到哪位数学家可以与之匹敌。他是解析几何的发明者之一；概率论的主要创始人；以及独承17世纪数论天地的人。一代数学大师费马堪称是17世纪法国最伟大的数学家。尤其他提出的费马大定理更是困惑了世间智者358年。