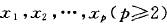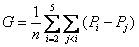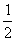岁月论坛

当前位置：首页 > 论文 > 理学 > 数学

以正方形为载体的中考试题赏析

来源：岁月联盟作者：苏兴震时间：2010-07-10

　　正方形是初中数学的重要知识内容，纵观2008年全国各地中题，可以发现诸多以正方形为载体，结合其它数学知识的优秀试题，格调清新、构思巧妙，较好的考察了学生的基础知识、学习能力和思维水平.现拮取几例加以赏析：

　1 与拼图相结合,注重考察学生的观察能力.

　例1 (湖南湘潭市)如图1，将一副七巧板拼成一只小猫，则下图中 ∠AOB=　　.

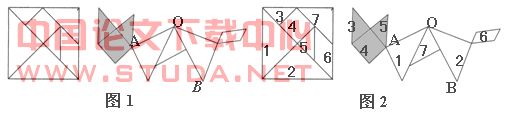
　解析观察发现这里正方形内的七巧板有5块是等腰直角三角形，1块正方形和1块锐角为45°的平行四边形。利用数字标出组成正方形和小猫的七巧板之间的对应关系，如图2所示，∠AOB内部的两块是等腰直角三角形，则∠AOB = 90°.

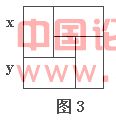
　例2 (湖北荆门市)用四个全等的矩形和一个小正方形拼成如图3所示的大正方形，已知大正方形的面积是144，小正方形的面积是4,若用x，y表示矩形的长和宽(x＞y)，则下列关系式中不正确的是( )　

　　(A) x+y=12 ． (B) x－y=2． (C) xy=35． (D) x＋y=144．

　　解析观察拼图3可发现:大正方形的边长是矩形的长和宽之和；小正方形的边长是矩形的长和宽之差.由大正方形的面积是144可知其边长是12,即x+y=12①；由小正方形的边长是4可知其边长是2,即x-y=2②,因此选项A和B的关系式均正确. 解①、②得x=7,y=5.因此：xy=35, x＋y=74.所以答案为选择D.

　　点评例1、例2的拼图试题在教材中是具有相应原型的，这里改编成中考试题可谓老树发新枝。事实上学生若能认真观察图形的本身特点进而找到相应数量关系，准确解答并不是件难事。

　　2 与多边形、圆相结合,注重考察学生对几何性质的综合运用.

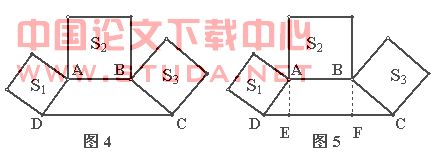
　　例3 (陕西省)如图4，梯形ABCD中，AB∥CD，∠ADC+∠BCD=90°，且DC=2AB，分别以DA、AB、BC为边向梯形外作正方形，其面积分别为S1、S2 、S3，则S1、S2 、S3之间的关系是．

　　解析此题中所求三个正方形的面积S1、S2 、S3之间的关系实质是求梯形ABCD的两个腰长及上底边边长

　　三者的平方关系.可利用梯形的高来建立桥梁

　　作用.如图5，分别过点

　　A、B做AE⊥DC,BF⊥DC,

　　垂足分别为E、F.设

　　梯形ABCD的高为h ,

　　AB=a, DE=x,则DC=2a,FC=a-x.由于∠ADC+∠BCD=90°，可证得△AED∽△CFB，有h2=ax-x. S1= AD2=h2+x2=ax,S2=a2,S3=BC2=h2+ (a－x)2 = a2－ax.因此:S1+ S3= S2.

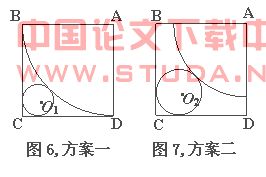
　　例4 (江苏南通市)在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他们首先设计了如图6所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图7所示的方案二．（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切．方案一中扇形的弧与正方形的两边相切）

　　（1）请说明方案一不可行的理由；

　　（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由．

　　解析 (1) 因为扇形ABC的弧长＝×16×2π＝8π，因此圆的半径应为4cm．由于所给正方形纸片的对角线长为 cm，而制作这样的圆锥实际需要正方形纸片的对角线长为 cm，由于，所以方案一不可行．

　　(2)设圆锥底面圆的半径为r，圆锥的母线长为R，则①,②,由①②，可解得，．故所求圆锥的母线长为 cm，底面圆的半径为cm．

　　点评将正方形与多边形、圆结合是中考中出现频率较高的题目。此类题目涉及知识点较多，跨度较大，需要学生具有较为扎实的基本功，具有综合运用相关数学知识的能力。

　　3 与“动点问题”相结合,注重考察学生对不变因素的探究能力.

例5 (湖北武汉市)正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD于点F。如图8，当点P与点O重合时，显然有DF＝CF．

　　(1)如图9，若点P在线段AO上（不与点A、O重合），PE⊥PB且PE交CD于点E.

①求证：DF＝EF；

②写出线段PC、PA、CE之间的一个等量关系，并证明你的结论；

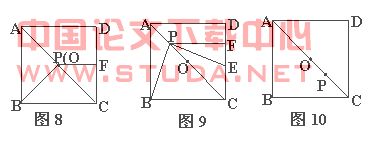
　　(2)若点P在线段OC上（不与点O、C重合），PE⊥PB且PE交直线CD于点E。请完成图10并判断(1)中的结论①、②是否分别成立？若不成立，写出相应的结论（所写结论均不必证明）

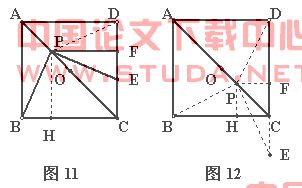
　　解析 (1) ①如图11过点P做PH⊥BC,垂足为点H,连接PD.此时四边形PFCH为正方形.容易证出△APB≌△APD,推得 ∠BPC=∠DPC，进一步可得∠BPH =∠DPF；由∠BPH +∠HPE =90°,∠EPF + ∠HPE=90°，得∠BPH =∠EPF.因为PE⊥DC,可证得DF=FE.

　　②由EF+CE=PC得:DF=EF=PC－EC.因为PF∥AD,有,将DF= PC－EC代入得: PC=PA+CE.

　　(2)连接PB、PD,做PF⊥DC, PH⊥BC,垂足分别为F、H,在DC延长线上取一点E,使得PE⊥PB.此时有结论①DF=EF成立.而结论②不成立, PC、PA、EC存在PA=PC+ EC关系.证明与②类似,略.

　　点评动点问题是中考热点问题之一，它要求学生善于抓住运动变化的性和不变因素，把握运动与静止的辨证关系.例5中,无论动点P在线段AC上如何运动, ∠BPE是直角以及四边形PFCH为正方形是不变的.

　　4 与对称、旋转相结合,注重考察学生变换的数学思想.

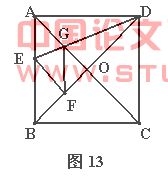
例6 （重庆市）如图13，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合.展开后，折痕DE分别交AB、AC于点E、G，.连接GF.下列结论：①∠AGD=112.5°；②tan∠AED=2；③S△AGD =S△OGD；④四边形AEFG是菱形；⑤BE=2OG.其中正确结论的序号是 .

　　解析由题意可知△AED和△FED关于ED所在的直线对称,有AE=EF,AG=GF,∠ADE=∠FDE=∠ADB=22.5°.则∠AGD= 180°－∠ADE－∠DAG=112.5°.由于易求得∠AGE= ∠AEG =67.5°,则AE=AG.因而,AE=EF=FG=AG,四边形AEFG是菱形.设AE=k,容易证得 △EFB和△OGF均是等腰直角三角形，则EB= k, OG = k.因此 EB=2OG.所以正确的结论是①、④、⑤，其余结论显然不成立。

　　例7 （黑龙江齐齐哈尔市）已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB,DC（或它们的延长线）于点M,N．当∠MAN绕点A旋转到BM=DN时（如图14），易证BM+DN=MN．

（1）当∠MAN绕点A旋转到BM≠DN时（如图15），线段BM,ND和MN之间有怎样的数量关系？写出猜想，并加以证明．

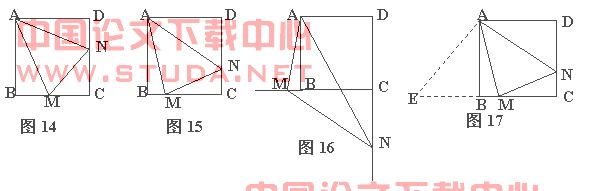
　　（2）当∠MAN绕点A旋转到如图16的位置时，线段BM,ND和MN之间又有怎样的数量关系？请直接写出你的猜想．

　　解析 (1)如图17，把△AND绕点A顺时针90°，得到△ABE，则有DN=BE,∠EAM= ∠MAN=45°.进而可证得：△AEM≌△AMN.所以MN=ME=MB+EB=MB+DN.

　　(2) 线段BM,ND和MN之间存在MN = DN－MB.

　　点评平移、翻折和旋转是初中几何重要的三种变换方式，变换之后的几何图形与原图形对应的边、角均相等.巧妙的运用变换的基本性质或构造变换图形，均可以使题目的解答简易而顺畅.

　　5 与函数图象相结合,注重考察学生的数形结合思想.

　　例8 （湖南长沙市）在平面直角坐标系中，一动点P（x，y）从M（1，0）出发，沿由A（－1，1），B（－1，－1），C（1，－1），D（1，1）四点组成的正方形边线（如图18）按一定方向运动。图19是P点运动的路程s（个单位）与运动时间（秒）之间的函数图象，图20是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.

　　（1）s与t之间的函数关系式是：；

　　（2）与图20相对应的P点的运动路径是：；P点出发秒首次到达点B；

　　（3）写出当3≤s≤8时，y与s之间的函数关系式，并在图16中补全函数图象.

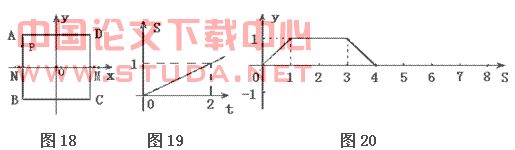
　　解析（1）图19是正比例函数图象，易求得s与t之间的函数关系式为：S= (t≥0)

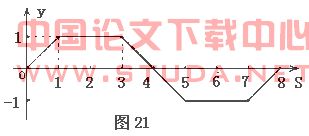
　　（2）从图20的函数图象可以看出，动点P的纵y在运动时随时间t的增大开始时逐渐增大，而后又不变，最后又减小至0，说明P点在正方形的运动路径是：M→D→A→N.由图18、19可知，P点从点M运动到点B的路程为5，速度为0.5，所以首次到达点B需要时间为10秒.

　　(3)结合图18和图20，分析可得，第1秒之前，动点P从点M向点D处运动；第1至3秒时，动点P从点D向点A处运动；第3至5秒时，动点P从点A向点B处运动；第5至7秒时，动点P从点B向点C处运动；第7至8秒时，动点P从点C向点M处运动.时间段不同，函数关系不同，因此列分段函数为：当3≤s＜5，y= 4－s；当5≤s＜7，y=－1；当7≤s≤8，y= s－8．补全的函数图象如图21.

　　点评函数图象问题是数形结合的数学思想的重要体现，在中卷中也往往作为具有一定区分度的题目出现。例8是一个分段函数问题，其关键是依据函数图象弄清楚点P在正方形ABCD上的哪一段运动,坐标与时间、路程如何变化.

　　6 与实际问题相结合,注重考察学生构建数学模型的能力.

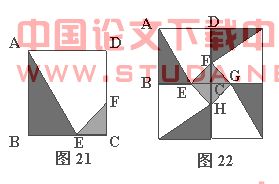
　　例9 （湖北荆门市）某人定制了一批地砖，每块地砖（如图21所示）是边长为0.4米的正方形ABCD，点E、F分别在边BC和CD上，△CFE、△ABE和四边形AEFD均由单一材料制成，制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元，若将此种地砖按图22所示的形式铺设，且能使中间的阴影部分组成四边形EFGH．

　　(1)判断图22中四边形EFGH是何形状，并说明理由；

　　(2)E、F在什么位置时，定制这批地砖所需的材料费用最省？

　　解析：(1) 四边形EFGH是正方形．图22可以看作是由四块图21所示地砖绕C点按顺时针方向旋转90°后得到的,故CE=CF =CG=CH．因此△CEF是等腰直角三角形.所以因此四边形EFGH是正方形.

　　(2)设CE=x米, 则BE=（0.4－x）米,每块地砖的费用为y,有：y= x ×30+ ×0.4×(0.4-x)×20+[0.16- x - ×0.4×(0.4-x)]×10= 10(x -0.2x+0.24) = 10［(x-0.1)²+0.23］(0＜x＜0.4).所以当x=0.1米时,y有最小值,即费用为最省,此时CE=CF=0.1米．