Malthus和Logistic模型及其医学应用
【摘要】 Malthus模型和Logistic模型是种群生态学的核心理论之一,它们在医学中的应用涉及传染病模型、肿瘤生长、肿瘤等。介绍了Malthus模型和Logistic模型在医学中的主要应用。
【关键词】 Malthus模型 Logistic模型 医 肿瘤
Abstract In this paper, Malthus model and Logistic model is among key theories of population ecology. Extensive research has been conducted on models, many applied to the field of the increase of cancer, epidemics, etc.
Key words malthus model; Logistic model; medical; cancer
1 Malthus 模型
1.1 Malthus 模型
Malthus模型[1~4]是由英国统计学家马尔萨斯(T R Malthus)于1798年提出的人口模型:
dN(t)dt=rN(t), N(t=t0)=N0 (1)
式中r 代表出生率,假设为常数,N(t) 为t 时刻的人口数量。方程(1)的解为:
N(t)=N0er(t-t0)(2)
模型(2)表示人口增长将按指数增长,称为Malthus人口指数增长模型,简称Malthus模型。实践证明当人口数量不太大时,Malthus模型能够很好的说明人口总数的增长情况。
1.2 流行病与传染病的Malthus 模型
Malthus模型在流行病与传染病预防方面具有一定的。设某地区的人口数为n ,初始时刻t=t0 共有i0 个人得了某种传染疾病,t时刻已感染(infective)的病人数为i(t) 。假定每一感染者在单位时间内将疾病传播给k 个人,并且该疾病既不会导致死亡也不会康复,则有与(1)式相同的模型[1],其解仍为(2)式。式中r 在医学上被称为该疾病在该地区的传染强度,假设为常数。一般地,传染病流传初期,该疾病既不会导致死亡也不会康复,用Malthus模型来描述在医学上有一定的参考价值,但随着时间的推移,它将越来越偏离实际情况。
1.3 肿瘤生长的Malthus模型
假设某肿瘤t 时刻的体积为V(t) ,初始时刻t0 的体积为V0 ,单位时间内肿瘤的增长率为r (r常数),并且肿瘤的增长率(体积变化率)与当时的体积成正比,则有如下方程[2]:
dV(t)dt=rV(t), V(t=t0)=V0 (3)
方程(3)的解为V(t)=V0er(t-t0) ,即肿瘤的增长也符合Malthus模型。在临床应用方面,肿瘤体积增大一倍所需要的时间t′(倍增时间)是刻划肿瘤生长的一个重要参数,不难得到:
t′=ln 2/r(4)
由于肿瘤的增长率r 往往不容易得到,而利用影像技术比较容易测出肿瘤的直径D ,所以临床上是将肿瘤近似地看成一个球体,利用体积公式V=43πR3= π6=D3,可得 D=D0er(t-t0)3
D=D0eln2t′gT3=D0(eln2)T3t′=D02T3t′=D02k3 (5)
其中T=t-t0=kt′,k 为倍增次数。取对数
k=3lg(DD0)/ lg2 (6)
转化为体积可得
k=lg (VV0) / lg2 (7)
当V=2V0 时,DD0=213≈1.26 。
一个癌细胞的直径约为10μm ,重约0.001μg 。假设肿瘤按Malthus模型指数增长,恶性肿瘤由初始的一个癌细胞到临床上可以检测出的直径1cm 肿块时,直径增大了1000倍,需要的倍增次数约为30。从直径约为10μm 、重约0.001μg 增大到直径1cm 的肿块,其重约为1g 。而从直径1cm 到致人死亡的1kg 重的癌症肿块,体积增大1000倍,需要的倍增次数约为10。这说明,癌症在发现前的平均增长期约为发现后的平均存活期的3倍。故及早发现及及早治疗在癌症治疗中起着至关重要的作用。
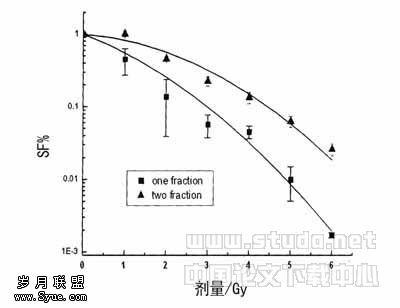
Skiper等人用老鼠做试验,研究了放射性治疗杀灭白血病细胞的规律,发现按照Malthus 模型指数增长的肿瘤经化疗后也按Malthus 模型指数规律消退,即V(t0+Δt)=V(t0)e-λΔt ,其中 Δt为放疗时间,λ>0 与放疗剂量有关,t0 为开始放疗时刻。由此他们提出了临床上一直使用的"对数杀灭"概念。设放疗的杀灭率为F ,则
F=1-V(t0-Δt)V(t0)=1-e-λΔt(8)
若杀灭率为0.9,则残存率为0.1,医学上称为一个对数杀灭;若杀灭率为0.99,则残存率为0.01,医学上称为两个对数杀灭;若残存率为10-k ,则医学上称为k 个对数杀灭等等。
1.4 药物在体内分布的Malthus 模型
在快速静脉注射时,设药物的总量为N0 ,药物在瞬间被注入体内,机体的体积设为V ,t时刻体内药物总量为N(t) 。假设机体内的药物分布是均匀的,药物的分解与排泄与当时体内的药物成正比(比例系数为r, r>0 ),对于机体来说,只有药物的输出而没有输入,于是可得与(1)式相同的模型,其解仍为(2)式。即在快速静脉注射方式下药物在体内的分布为负增长率的Malthus模型[2]。通常药物在体内的浓度C(t)=N(t)/V=e-nN0/ V 被称为是血浆药物浓度,简称血药浓度。医学上将血药浓度减少到一半所需要的时间t1/2 称为药物的半衰期,与(4)式类似地有t1/2=ln2/k 。
2 Logistic生长模型
在Malthus 模型(2)中,模型的增长是以er 为公比,按几何级数无限增长。这与实际是不符合的。因为流行病与传染病的Malthus模型、肿瘤生长的Malthus模型等不可能无限制地增长。因此,应该对Malthus模型中关于增长率为常数这一假设进行修改。Logistic模型是由Verhulst于1838年提出的,也就是人们常称之为逻辑斯谛方程。
2 经典的Logistic模型
通过分析不难发现,当人口稀少从而资源相对较为丰富,人口增长得较快。当人口数量到一定水平后,会产生许多新问题,如食物短缺、居住和拥挤等,此外,随着人口密度的增加,传染病会增多,死亡率会上升,所有这些都会导致人口增长率的减少,即诸多因素对人口的增长起着阻滞的作用,并随人口的增加,阻滞作用越来越大。在一定的环境内,对Malthus模型的基本假设进行修改,作以下的假设:
① 种群的个体不区分大小,分布是均匀的,且系统是封闭的,即没有迁出和迁入发生;
② 环境内资源的供给始终保持一个常数,且对每一个个体的分配是均等的;
③ 种群具有并保持稳定的年龄分布,种群每个个体具有相同的增长率;
④ 环境提供给种群生存和繁殖的资源是有限的。
Verhulst假设人口的相对增长率为:
1/ N·dN(t)/dt=r(1-N/K) (9)
或 dN(t)/dt=rN(1-N/K)(10)
方程(9)或(10)称为Logistic方程[1~3]。其中常数r>0 称为内稟自然增长率(intrinsic rate of natural increase),它表示每个个体在没有受到抑制作用时的最大增长率,也就是该种群个体的平均出生率与死亡率之差,反映了种群的内在特征。K>0 反映了环境资源的丰富程度,当N=K 时,种群不再增长。因此,K 表征了环境能容纳此种群个体的最大数量,称为环境的容纳量。
Logistic方程(9)可以作如下的解释:人口相对增长率应当是人口数量的函数r(N) ,随着人口数量的增加r(N) 将减少,则r(N) 应是减函数,最简单的减函数是线性函数,因此设
r(N)=r-sN (11)
当N=K 时人口不再增长,即r(K)=0 ,代入(11)式得s=r/K ,于是(11)式为:
r(N)=r(1-N/K) (12)
方程(9)的另一种解释为:由于资源最多仅能维持 K个个体,故每个个体平均所需要的资源为总资源的1/K 。在 tt时刻N(t) 个个体共消耗了总资源的N(t)/K ,此时剩余为1-N(t)/K 。因此,种群的相对增长率与当时所剩余的资源份量成正比。这种种群密度对种群规模增长的抑制作用,称为密度制约(density dependence)。当不考虑密度制约因素时,Logistic方程就变成了Malthus方程。
方程(10)的解释为:当人口数量较大时,种群间会发生生存竞争,并导致增长率降低。竞争的强弱既和当前的种群数N(t) 有关,又和环境还能供养多少种群K-N 有关,因而和两者的成积成正比。
对剩余资源1-N(t)/K 的分析:
① 如果种群数量N(t) 趋于0,那么(1-N(t)/K )项就接近于1,这表示几乎全部K 空间尚未被利用,种群接近于指数增长,或者说种群潜在的最大增长能充分实现。
② 如果种群数量N(t) 趋于K ,那么(1-N(t)/K )项就接近于0,这表示几乎全部K 空间已被利用,种群潜在的最大增长不能实现。
③ 当种群数量N(t) 由趋于0逐渐地增加到K ,(1-N(t)/K )项则由1逐渐地下降到0,这表示种群增长的剩余空间逐渐变小,种群潜在的最大增长的可实现程度逐渐降低。
方程(10)是一个可分离变量的方程,容易求出它满足N(t0)=N0 的解析解为:
N(t)=K1+(K/N-1)e-r(t-t0) (13)
2.2 肿瘤生长的Logistic模型
在肿瘤增长的过程中,由于营养供应有限,将会阻滞肿瘤细胞的增长速度,研究发现,对中晚期肿瘤增长的更好描述是使用Logistic模型[2],假设V(t) 为t 时刻肿瘤的体积,则有:
dV(t)/dt=rV(t)-λV2(t)(14)
若设K=r/λ ,则方程(14)变成与方程(10)的形式。
2.3 传染病的SI模型
在传染病的Malthus模型中,假设条件修改为:
① 疾病在传播期内总人数不变,无死亡和迁移,人群分为易感染者(Susceptible)和已感染者(Infective),t 时刻两类人群的所占的比例分别为S(t) 和N(t) ;
② 每个病人每天有效接触的平均人数为λ ,称为日接触率。
则模型修改为dN(t)/dt=λN(t)S(t) ,将N(t)+S(t)=K 代入即得到传染病的SI模型[1]:
dN(t)/dt=λN(K-N),N(0)=N0 (15)
2.4 Logistic模型的稳定性
设模型为:
dN(t)/dt=NF(N)(16)
定理[4] 如果函数F(N) 满足下列条件,则模型(16)是全局稳定的:
① 有一个正的平衡点N*>0 ,即有N*0 ,F(N*)=0 ;
② 对于0
③ 对于N>N* ,有F(N*)>0 。
对于Logistic模型dN(t)/dt=rN(1-N/K) ,由定理可知,它是全局稳定的。即当种群的数量在受到干扰后,经过一定的时间TR ,种群数量还将恢复到平衡位置。一般来说,干扰的大小会影响TR 的数值大小,这个时间TR 称为特征返回时间,May等人研究得到 TR≈1/r 。
【】
1 姜启源.谢金星等.数学模型.第3版.北京:高等出版社,2003,9~15;135~200.
2 杨启帆.数学建模.北京:高等教育出版社,2005,50~90.
3 余爱华.Logistic模型的研究.南京,南京林业大学硕士研究生学位,2003.
4 陈兰荪.数学生态模型与研究方法.北京:出版社,1998,1~50.