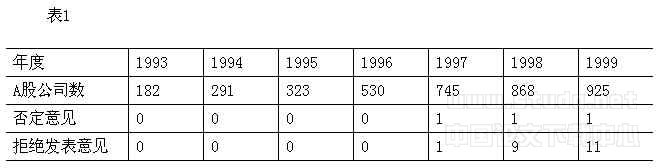
商业银行信贷风险计量模型应用研究
摘 要:在商业银行信贷风险计量模型中,均值—方差模型可用于对信贷资产价值的波动趋势和方向的计量,?鸦VaR:CreditMetrics模型能够相对准确地计量出信贷资产价值的波动程度,它既可以计量一种信贷资产的风险度,亦可计量多种信贷资产的组合风险度,具有较强的可操作性;KMV模型只有在计量样本数足够多的信贷资产组合的价值波动程度的时候,才比较准确和可行。
关 键 词:信贷风险;计量模型;均值;方差;在险价值
众所周知,呆坏账的产生和积累是导致商业银行资产质量低劣的直接诱因。如何正确地计量信贷风险,应成为我国商业银行关注的问题之一。然而,目前我国的商业银行对信贷风险的控制还处在初级阶段,主要是根据部分财务指标来判定信贷风险是否存在,或根据贷款五级分类法对信贷进行分类后跟踪管理等,而对信贷风险的程度大小,则欠缺准确的计量。本文主要研究了均值—方差模型、在险价值VaR?押CreditMetrics模型和期权推理分析KMV模型,
并利用它们对一些信贷资产的风险程度进行了模拟计量。
一、均值-方差模型
均值-方差模型涉及的一个重要概念是分布函数,用以对事件发生的概率进行完整的描述。分布函数是描述事件随机取值的统计工具,它表示随机变量在各个范围内取值的概率,如变量ξ的分布函数为:F(x)=P(ζ
然而,在实际工作中,确定一个事件的分布往往十分困难,而且有时也无必要。因此,人们进一步采用均值和方差来描述事件的特征。均值是事件的每一个可能取得的收益的加权平均数,它反映出一个资产的预期收益。均值越大,表明预期收益越大;反之则反。假设收益R取值ri(i=1,2,┈,n)时的概率为pi,则收益的均值μ为:
μ=piri (1)
如在表1中,收益的均值为:
μ=(-0.15)×0.1+(-0.10)×0.15+0×0.2+0.10
×0.25+0.15×0.2+0.2×0.1
=0.045。
方差σ2(或标准差σ)反映事件的实际值与其均值的偏离程度,其公式为:
σ2=pi(ri-μ)2(2)
或σ= (3)
如表1中,方差为:
σ2=(-0.15-0.045)2×0.1+(-0.10-0.045)2×
0.15+(0-0.045)2×0.2+(0.10-0.045)2×
0.25+(0.15-0.045)2×0.2+(0.20-0.045)2×
0.1
=0.0128
方差反映了事件发生结果的波动状况,从而可以用来揭示资产收益的变动幅度,即估量金融风险的大小。方差越大,说明事件发生结果的分布越分散,资产收益波动越大,金融风险越大;反之,方差越小,金融风险越小。
此外,在实际业务中,由于风险往往是针对损失而言的,人们更关心收益小于均值时的分布情况。因此,这里引入偏方差(σ2-)的概念:
σ2-=pi(μi-μ)2
式中的μi为小于μ的m种收益,用来描述小于均值的收益的波动情况。
然而,均值—方差模型只能让人把握信贷风险的一般水平和方向,对于风险值的大小,则无能为力。这便是其局限性。
二、在险价值VaR:CreditMetrics模型
利用CreditMetrics模型计算在险价值VaR是最有影响的方法之一。该模型的基础是在给定的时间段内估计贷款及债券产品资产组合将来价值变化的分布状况。价值变化与债务人信用质量的转移(信用评级是上升,是下降,还是违约)相关。
(一)用CreditMetrics模型度量一种信贷资产的VaR值
度量一种信贷的VaR值分为四个步骤:第一,确立评级体系及借款人从一个信用级别转移到另一个信用级别的概率。第二,利用贴现法计算贷款的现值。第三,算出将来信用转移后资产组合价值变化分布。第四,计算在一定置信度下的VaR值。
第一步,确立转移矩阵。转移矩阵,是指信贷和债券从一个信用级别转变为另一个信用级别的概率。穆迪和标准普尔等评级机构均有这方面的数据积累(见表2)。从该表可以看出,一家停留在原信用等级的可能性最大,转移到离原信用等级越远的信用等级的可能性越小。
第二步,利用合同现金流贴现法计算贷款的当前市场价值。借款公司信用等级的上升和下降必然影响到风险贷款的信贷差价。因此,也影响到贷款的潜在市场价值。根据合同现金流贴现法,可以重新估价贷款的市场价值。其中要用到贴现率(见表3)。
假如一项对信用等级BBB级企业的五年期贷款100亿元,合同利率为6%,而在一年期末,其信用等级发生了改变,假如从BBB级下降到BB级,那么,其一年期末的风险贷款的现值和市场价值为:
VBB=6++
=6+
=102.02(万元)。
其中,每年支付的利息为6万元,最后一年支付本金100万元和利息6万元;贴现率为ri+si,ri为一年期无风险利率,si为由于贷款信用等级的变化而产生的贷款的一年期、二年期、三年期、四年期的贷款差价。
假如该公司一年末仍然是BBB级,那么,该风险贷款的折现值为:
VBBB=6+
=107.5(万元)。
第三步,计算信用转移后资产组合价值变化分布。如果对每一级别重复上述贴现值计划,就可以得到一年后不同级别债券的一系列现值,即可得市场价值分布情况(见表4)。
第四步,计算一定置信度下的在险价值VaR。从表4可见,价值变化△V分布的第一个分位数为-23.91,这也是99.82%置信度下的VaR值。
如果假设△V服从正态分布的话,99%置信度下的VaR值的计算过程为:
设△V的均值为μ,样本标准差为σ。
则 μ=∑piΔvi
=0.02%×1.82+0.33%×1.64+……+
0.18%×(-56.42)
=-0.46
σ2=∑pi(Δvi-μ)2
=0.02%×(1.82+0.46)2+0.33%×
(1.64+0.46)2+……+0.18%×
(-56.42+0.46)2
=8.95
σ=2.99
正态分布N(μ,σ2)的置信度1-α=99%的最大在险价值VaR值[1]64为:
x1-α=-
=-2.58×
=-2.73
式中,为从“正态分布数值表”中查出的99%置信度下的积分上限值。
以上是对单一信贷资产的VaR值进行的,下面将对两种和多种信贷资产组合的VaR值进行计算。假设把初始评级分别为BB和A两个债券组成的资产组合。转移矩阵如表2所示,假设两者之间没有相关性,即相关系数为0,根据联合转移概率公式P=PBBPA计算出表5中的BB级和A级债券零相关性下的联合转移概率矩阵。
表6列出了BB级和A级债券相关系数为20%时的联合转移概率矩阵。
进一步,我们可以用(1)、(2)、(3)式计算出μBB、μA、σB、σA等变量,然后再用下述模型分析两种产品构成的资产组合的风险及其在险价值VaR。假设这两种产品构成的资产组合Z(其中产品BB、A的比重分别为x、y)的均值μz和方差分别为:
μz=xμBB+yμA
=x2+2xyσBBA+y2
=x2+2xyρσBBσA+y2
式中,μBB、μA、σA、σBBA分别是产品BB、A的均值、标准差和两者的协方差(即两者的联合转移概率);ρ是这两种产品的相关系数,它表示两种资产的相互关联程度。
对于更多种产品,比如n种产品X1,X2,…,Xn的组合,我们仍可以算出其均值μ和方差σ2:
μ=xiμi
σ2=+2ρijxixjσiσj
其中,xi是第i种资产在总组合中所占的比例,μi、分别为第i种资产的均值和方差,ρij是第i种资产和第j种资产的相关系数。与单种资产一样,资产组合的总体方差越大,表示该组合的总体风险越大;反之则反。
将上述σz的σ或值带入下列公式,即可得出:
VaR=-
式中,是资产组合在1-α置信度下从“正态分布数值表”中查出的积分上限值,n为某资产向其他所有资产转移的种类数,比如在表5和表6中,n为8。
当然,CreditMetrics模型也有自己的局限性,即在分析信用风险时假设信用风险独立于市场风险,而实际上信用风险和市场风险是相互交织在一起的,也存在相互影响关系。
三、期权推理分析法:KMV模型
期权推理分析法:KMV模型,是著名的风险管理公司KMV公司研究出的风险计量方法。该方法假设公司负债主要是借入的银行贷款,记为K;公司资产的市场价值为A。在贷款期限内,当A发生贬值,并且使A
E=f(A,σA,K,r,t)
式中,A——资产的市场价值;
σA——资产市场价值的标准差;
K——银行贷款金额,即违约点;
r——无风险利率;
t——贷款到期的期限。
首先,是计算资产市场价值的标准差σA,它一般是未知的。1986年学家Ronn和Verma设计出计算σA的模型为:
σA=ησE
其中,η是所有者权益对企业资产的弹性系数:η= ,V是企业资产的当期价值;σE是所有者权益的标准差。
其次,是计算违约距离DD(Distance to Default)。违约距离是资产价值A与违约点K的距离。这个距离越小,违约风险越大。其计算公式为:
DD=
再次,是计算期望违约频率EDF(Expected Default Fre-quency)。它是位于违约点以下的面积的大小,即概率的大小。其公式为:
EDF=φ(-DD)
比如,当计算得DD为2时
EDF=φ(-2)=1-φ(2)=2.275%
式中的φ(2)可以从“累计正态分布数值表”中查出,为97.725%。φ(-2)表示资产价值小于违约点或应归还贷款金额的概率或频率。
最后,期望损失额EL(Expected Loss)。不过在此之前应该已知或计算出恢复率RV(Recovery Rate)和违约后损失率LGD(Loss Given Default)。恢复率是指违约发生之后,所能够偿还部分占贷款总额的百分比。违约后损失率是指违约发生后,损失金额占贷款总额的百分比。因此,LGD=1-RV。这样,期望损失可以采用下述公式计算:
EL=EDF×LGD×RE
式中,RE(Risk Exposure)为信贷的风险暴露额,一般就是可能经受损失风险的贷款金额。
当然,任何事物都有其两面性,比如期权推理分析法KMV模型,就拥有下列局限性:
第一,它是在借款人未来资产的变化服从正态分布的假设下进行计算和分析的,如果该假设不成立了,就很难构造期望违约频率模型了。
第二,它没有对贷款资产区分等级,比如没有像大多数资产那样,区分出信用等级等。这忽视了不同贷款的不同个性,使计算结果的准确性受到影响。
第三,对于新成立的公司或者小公司,由于缺少足够的研究资料和数据,所以会使违约频率的计算难以进行。
四、结论
从以上分析来看,均值—方差模型可以用于对信贷资产价值的波动趋势和方向的计量;而VaR:CreditMetrics模型,则能够相对准确地计量出信贷资产价值的波动程度,而且既可以计量一种信贷资产的风险度,亦可计量多种信贷资产的组合风险度,具有较强的可操作性;KMV模型只有在计量样本数足够多的信贷资产组合的价值波动程度的时候,才比较准确和可行。
:
[1]茆诗松,王静龙.统计手册[M].北京:出版社,2003.
[2]P.Jorion,“Risk:Measuring the Risk in Value at Risk”, Financial Analysts Journal, November/December 1996.
[3]M.Carey,“Credit Risk in Private Debt Portfolios”,Journal of Fi-nance, vol.53, August 1998.
[4]Y.John Campbell,W.Andrew Lo,A.Craig Mackinlay,The Econo-metrics of Financial Markets, Princeton University Press,1997.
[5]J.Edwin Elton,J.Marin Gruber,Modern Portfolio Theory And Invest-ment Analysis,Fifth Edition,John Wiley & Sons,Inc.,1995.
[6]庄毓敏.商业银行业务与经营[M].北京:人民大学出版社,1999.
[7]章彰.商业银行信用风险管理——兼论巴塞尔新资本协议[M].北京:中国人民大学出版社,2002.
[8]张淼.商业银行信贷风险管理——模型、方法与建议[M].上海:上海财经大学出版社,2005.
[9]施兵超,杨文泽.金融风险管理[M].上海:上海财经大学出版社,2003.