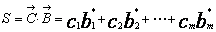摘要 该文以研究生教学质量评估为例,讨论了教师教学质量评价指标,采用层次分析法确定了各项指标的权值,给出了一个关于教师教学质量评价的模糊综合评价模型,利用VBA编程在Excel中实现模糊综合评价的。
关键词 教师教学质量,层次分析法,模糊综合评价,VBA,Excel
1 引言
在教育教学管理中,对教学质量的评价是必不可少的,而传统的通过初步的定量分析确定评价指标或根据调查表的分值进行加权求带有很大的主观片面性,缺乏坚实的基础。因此,利用层次分析法计算各项指标的权重,用模糊综合评价法来建立评价模型,使评价结果更科学有效。模糊综合评价方法是针对某些学位与研究生教育评估对象的复杂性及其评价指标模糊性,采用模糊数学的理论和技术对受多种因素影响的复杂的评估对象,进行综合评价,从而得到评估结果的方法。由于计算评价结果相对复杂和一定重复性,因此利用办公系统软件Office中Excel强大的VBA(Visual Basic Application)功能,利用编程实现计算,使计算方便快速,结果准确。
2 模糊评价的原理与数学模型
2.1 基本思想 模糊综合评价方法的基本思想是在确定评价因素、因子的评价等级标准和权值的基础上,运用模糊集合变换原理,以隶属度描述各因素及因子的模糊界线,构造模糊评判矩阵,通过多层的复合运算,最终确定评价对象所属等级。 首先是对最低层的诸项指标进行模糊综合评价,再对较高层次的诸项进行模糊综合评价,直到对最顶级指标进行模糊综合评价为止。如果有多类的评价人员,那么就综合多类人员的评价结果,根据最大隶属度原则,就可得到教师最后的定量评价结果。
2.2 数学模型 设指标集为
U={
U1,U2,…,Un},评语集为
V={
V1,V2,…,Vn},指标权系数子集为
W={
W1,W2,…,Wn},U的第i个指标对应的评语集V中的评价V
1,V
2,…,Vm的隶属度分别为r
i1,r
i2,…,r
im,U的这一指标U
i对于V中的每一种评价的隶属度组成了V上的模糊子集,记为R
i={r
i1,r
i2,…,r
im}。对于每一指标U
i(i=1,2,…,n)都求出对应的Ri,就构成了一个U×V上的模糊矩阵,即
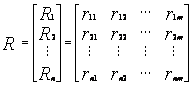 。
。
对矩阵W与R作模糊矩阵乘法得:
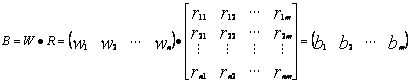
其中
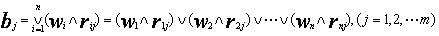
对B进行“归一化”处理,即得

,其中
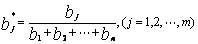
为了便于综合分析,要利用双权法把上述综合评价结果转化成相应的综合评价值。双权法即对j种评价赋以新的权系数
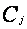
得到新的权重向量
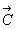
,且
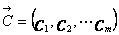
,将其乘以综合评价的向量
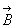
即可求得综合评价值为
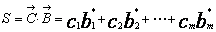
3 实际应用
教师教学质量模糊综合评价过程如下: (1) 建立教学质量的评估指标体系
评价教学质量的指标体系(以此为例,仅作)| 一级指标 | 教学质量F |
| 二级指标 | 教学素质F1 | 教学内容F2 | 教学方法F3 | 教学效果F4 |
| 三级指标 | 教学态度F11 | 教学组织F12 | 教学秩序F13 | 教书育人F14 | 教学大纲与目标F21 | 思想性和前沿性F22 | 系统性和科研性F23 | 理论联系实际F24 | 启发性授课方式F31 | 运用信息技术F32 | 形象生动灵活F33 | 指导学习方法F34 | 成绩 F41 | 课堂状况F42 | 学习方法 F43 | 练习作业F44 |
| | | | | | | | | | | | | | | | |
(2) 确定各项评价指标的权重利用层次分析法将各项评价指标计算出来的结果填到对应的表格中。 (3) 收集模糊评价信息 设计一份分好等级的调查表,让评价者对各指标作出等级评定,在评定的等级栏中划“√” 。
教学质量调查表(仅以“教学素质”为例)| 教学素质F1 |
| 教学态度F11 | 教学组织F12 | 教学秩序F13 | 教书育人F14 |
| 好 | 较好 | 一般 | 较差 | 差 | 好 | 较好 | 一般 | 较差 | 差 | 好 | 较好 | 一般 | 较差 | 差 | 好 | 较好 | 一般 | 较差 | 差 |
| | √ | | | | | √ | | | | √ | | | | | | | √ | | |
(4) 模糊综合评判
将所得的调查表结果统计填到表里,建立模糊集合进行计算。
按等级评价教学内容所属各指标的人数统计| 二级指标 | 三级指标 | 学生评价 | 同行评价 | 领导评价 |
| 50名 | 20名 | 5名 |
| 好 | 较好 | 一般 | 较差 | 差 | 好 | 较好 | 一般 | 较差 | 差 | 好 | 较好 | 一般 | 较差 | 差 |
| F1 | F11 | 25 | 16 | 8 | 1 | 0 | 16 | 3 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 |
| F12 | 24 | 16 | 7 | 2 | 1 | 4 | 5 | 8 | 2 | 1 | 4 | 1 | 0 | 0 | 0 |
| F13 | 18 | 18 | 11 | 1 | 2 | 12 | 4 | 4 | 0 | 0 | 3 | 1 | 1 | 0 | 0 |
| F14 | 21 | 16 | 4 | 8 | 1 | 11 | 6 | 3 | 0 | 0 | 3 | 2 | 0 | 0 | 0 |
4 在Excel中VBA编程计算的实现
(1)
将调查结果填入表格相应的位置。
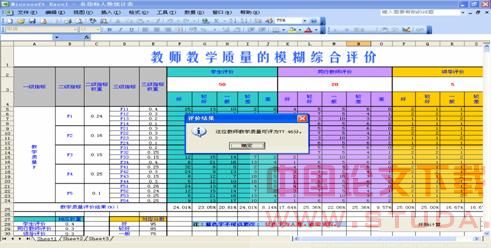
(2) 用VBA编程查找输入的各项结果和指标值,将他们存入变量。 根据表格中固定的信息利用
Range().Find()函数在特定的区域中查找所需要的值,如查找二级指标权重系数(其中
f2Name为固定信息“F1”)
Private Sub Find2w(f2Name As String) ……’此处略去变量定义 With Range("B1:B30")’确定所查找的范围 Set d =.Find(f2Name, LookIn:=xlValues) If Not d Is Nothing Then firstAddress = d.Address Do …… ’将查找到值赋给定义的数组变量 Set d = .FindNext(d)’查找下一个满足条件的数值 Loop While Not d Is Nothing And d.Address <> firstAddress End If End WithEnd Sub (3)某一类人群的模糊评价矩阵,以学生为例,
…… For i = 0 To iF1Count - 1'计算学生模糊评价 Find3w (strArrayF2w(i))’调用查找三级指标权重系数 ReDim fArrayE(iF2Count, 5)’重定义二维数组维数 iRow = 0 iNum = 5 + iF2Count * i '得到每一个F学生评价的范围 RangeField = "F" & iNum & ": J" & iNum + iF2Count - 1 For Each c In Range(RangeField).Cells’循环建立矩阵 fArrayE(iRow, iCol) = c.Value / iStudent iCol = iCol + 1 If iCol = 5 Then iRow = iRow + 1 iCol = 0 End If Next (4)根据得到的数值计算指标的模糊评价矩阵,以求二级指标的模糊评价矩阵为例。根据模糊矩阵相乘运算法则
Private Sub CalMohuN(iRow As Integer, iLoopNum As Integer) ……’此处略去变量定义 For j = 0 To 4 'fArrayF3w(i)*fArrayE(iRow, iCol)->模糊矩阵相乘 fMax = 0 For i = 0 To iRow If fArrayF3w(i) < fArrayE(i, j) Then fMin = fArrayF3w(i) Else fMin = fArrayE(i, j) End If If fMax > fMin Then fMax = fMax Else fMax = fMin End If Next i fArrayR(iLoopNum, j) = fMax fSum = fSum + fMax Next j For i = 0 To 4'归一化求二级指标的评价矩阵 fArrayR(iLoopNum, i) = fArrayR(iLoopNum, i) / fSum Next iEnd Sub (5) 结果输出 将计算出的二级指标评价填入相应的表格里,再根据三类评价者所影响的程度不同,按照模糊关系合成理论再进行模糊评价,并可根据最大隶属度原则得出该教师的评价结果。 为了得到更加明确的结果可以继续进行某种处理,可规定各等级对应的代表分数,并将由他们构成等级分矩阵乘以最终的模糊评价结果矩阵,可以得到该教师教学质量的最后得分。
5 目前对教师课堂教学质量的评价工作已是教学质量评价中不可缺少的一部分。模糊综合评判法克服了评价中的随意性,使目标更明确,步骤更清晰,它将定量与定性较好地整合起来,显示出其他方法无法比拟的优越性。其评价结果公正、客观公平。 由于模糊综合评判法涉及到很多的矩阵运算,其运算过程又比较繁琐,大量重复的数字在抄写和运算时也容易产生差错,尤其是评价人数较多时十分费时费力。近年来,随着计算机技术的,Office办公系统的广泛应用,利用其强大的VBA编程计算功能解决了这一问题。使用时只需打开已嵌入VBA的Excel,轻松地输入指标权重和评价结果,点击计算按钮,瞬间即可得到教师的综合评判的结果,为广泛应用模糊综合评判法提供了方便快捷的途径。
[1] 金娣,王刚.教学评价与测量[M].北京:科学出版社。[2] 刘本固.教育评价的理论与实践, 浙江教育出版社。[3] 姜启源.数学模型(第二版)[M].北京:高等教育出版社。[4] 贺仲雄.模糊数学及其应用,天津科学技术出版社。
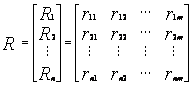 。
。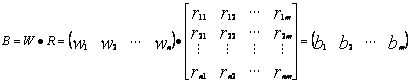 其中
其中 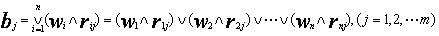 对B进行“归一化”处理,即得
对B进行“归一化”处理,即得 ,其中
,其中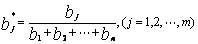 为了便于综合分析,要利用双权法把上述综合评价结果转化成相应的综合评价值。双权法即对j种评价赋以新的权系数
为了便于综合分析,要利用双权法把上述综合评价结果转化成相应的综合评价值。双权法即对j种评价赋以新的权系数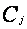 得到新的权重向量
得到新的权重向量 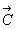 ,且
,且 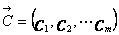 ,将其乘以综合评价的向量
,将其乘以综合评价的向量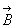 即可求得综合评价值为
即可求得综合评价值为