一道例题在中考压轴题中的应用

摘  要：本文选用了几个精彩的数学解题案例，笔者通过实例阐明了自己在数学教学中的看法，即例题教学是提高数学课堂教学效率的关键。

关键词：例题   几何教学    教学效率

数学课本是获取数学知识的主要源泉，课本中的例题与习题很好的体现了教学目标与学习目标，揭示了课本上基本知识最直接简捷的应用方法。有很大的引伸、变化、拓展的空间。在各地历年来的中卷中不乏以教材中例题或习题为原型加工的压轴题，北师大版八年级下册131页的引例就是一个被多次应用的题目。

一  课本例题

例一：北师大版八年级下册131页例

如图，在等腰△ABC中，底边BC=60cm，高AD=40cm，四边形PQRS是正方形。

（1）△ASR  与△ABC相似吗？为什么？

（2）求正方形PQRS的边长。

           评析：本题具有一定的代表性，本图形也是非常典型的基本图形。事实上，四边形PQRS是△ABC的内接四边形。

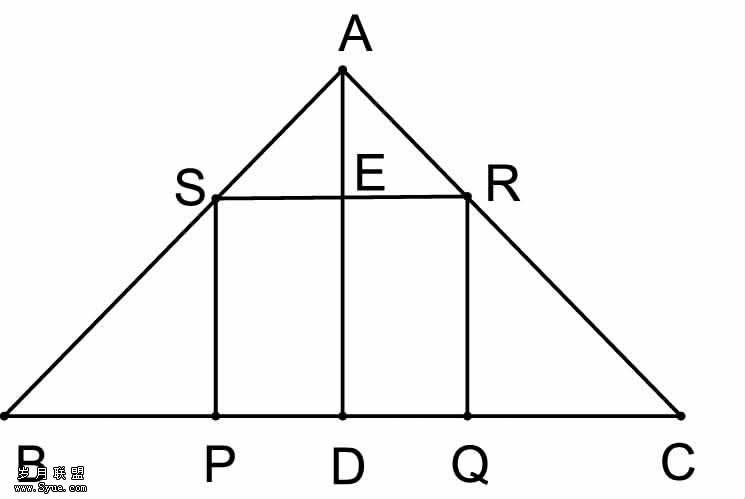
本题旨在考察： 1、相似三角形的判定；

2、相似三角形的性质：相似三角形对应高的比等于相似比。

解析：（1）略

(2) ∵ △ASR∽△ABC     ∴

∴ 设正方形的边长为x cm，则AE=(40-x) cm.,

∴      ∴ x=24       ∴设正方形的边长为24cm..

例二、北师大版九年级下册62页例

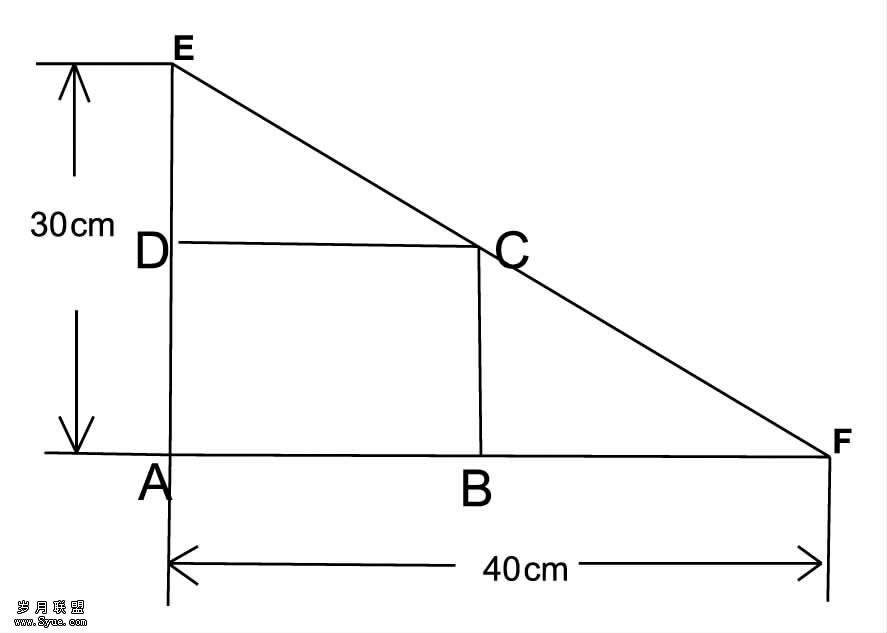
如图，在一个直角三角形的内部作一个矩形ABCD，其中AB和CD分别在两直角边上。

    （1）设矩形的一边AB=xm，那么AD边的长度如何表示？

（2）设矩形的面积为ym²，当x取何值时，y的值最大？最大值是多少？ 

评析：本题在上例的基础上稍有变化，内接四边形由正方形变为矩形，因此AB与 AD边长不再相等，但仍然可以运用上例的方法求解。

（1）要求AD边的长度，即求BC边的长度，而BC是△FBC中的一边，因此可以用三角形相似求出BC．由△EBC∽△EAF，得 所以AD=BC= (40-x).

（2）第 (2)问在（1）的基础上，要求面积的最大值．要求面积就需要求矩形的两条边，把这两条边分别用含x的代数式表示出来，代入面积公式就能转化为数学问题了，即求函数y=AB·AD=x· （40-x)的最大值，利用二次函数的知识迎刃而解．

二、中考题展示

例一 ．已知抛物线y=ax²+bx+c（a 0）与x轴交于不同的两点A（x₁，0）和B（x₂，0），与y轴的正半轴交于点C。如果x₁，x₂是方程x²-x-6=0的两个根（x₁＜x ₂）,且△ABC的面积为 。

(1)求此抛物线的解析式；

（2）求直线AC和BC的解析式；

（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作直线PQ∥x轴，与直线BC交于点Q，则在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出等腰直角三角形的直角边长；若不存在，请说明理由。

评析：此题第三问求直角边长，若直角顶点为P（或Q）,可划归为例一的基本图形求解；若R为直角顶点，可划归为例二求解。

解析（1）抛物线的解析式为 y=- x²+ x+3

（2）l_AC: y= x+3              l_BC: y=-x+3

    （3）存在；分三种情况

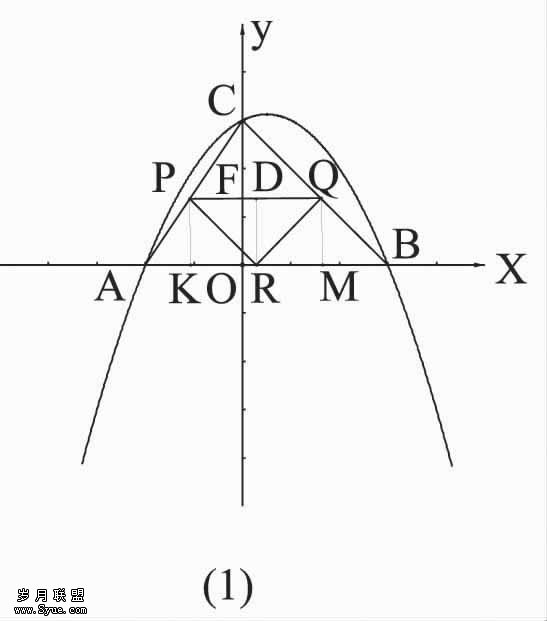
    ① 如图（1），若直角顶点为P（或Q）,作PK⊥AB，QN⊥AB

若PQ=PK，则△PQK为等腰直角三角形，此时，四边形PQDR为正方形，设PQ=x,

∵△CPQ∽△CAB,    ∴    

∴    ∴ x=    即PQ=PK=

②如图（1）,同理可得PQ=QN=

③如图（2），若R为直角顶点，PR=RQ，

则△PQR即为等腰直角三角形，此时，矩形

PQDE的长与宽的比为2︰1（PQ︰PK=2︰1）

设PK=x，则PQ=2x，

    ∵ △CPQ∽△CAB    ∴ 可得x=     ∴ 直角边PQ= · =

综上所述：直角边长为 或

例四．如图，已知⊙O₁与⊙O₂内切于点A, △ABC是⊙O₂的内接三角形，AB,AC分别交⊙O₁于点F,G. EF⊥BC于E,GH⊥BC 于H ，AD是△ABC的高，AD=6,BC=8.

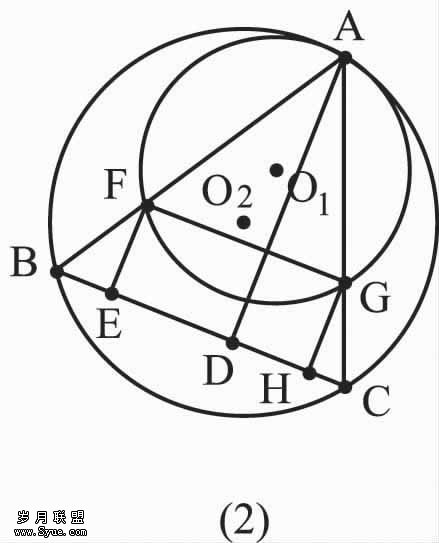
(1)  求证：四边形EFGH是矩形；

(2)  设EF =x,写出矩形EFGH的面积y与x之间的函数关系式，并求出自变量的取值范围；

(3)  当矩形EFGH的面积最大时，两圆半径有什么关系？证明你的结论。

     评析：此题综合性较强，考察到了圆、三角形、四边形的相关知识，图形较复杂，但是矩形EFGH仍是△ABC的内接四边形，掌握好了基本图形，容易解决。

当然，并非所有的题目都要使用这一方法，在解题时必须慎重审题，力求找到最佳的解题方法。不可盲目套用程式，简单模仿经验，造成思维定势，不利于对知识的迁移能力的培养。

总之，例题教学是数学教学的重要环节，特别是几何中基本图形的教学，必须引导学生熟记、理解、掌握，并要灵活运用，这是提高教学效率的关键。在中考复习中，如果能“以本为纲，紧扣教材”，从课本例题与习题入手，掌握基本方法，并进行探究，定会取得事半功倍的效果。