高职数学教材编写的思考与探索

　　摘要：高职数学教材的编写应以应用能力培养为主线，采用模块编写方式，将数学建模的思想与方法融入其中，兼顾人文，以“问题情境—展现知识—实现应用”的思路呈现教学内容。
　　关键词：高职；数学教材；应用能力；数学建模；人文教育
　　
　　自20世纪90年代始，我国的高职教育呈现出前所未有的势头，至2005年底，全国已有高职院校一千多所。高职院校的快速发展，一方面最大限度地满足了国民接受高等教育的强烈愿望，产生了可观的社会效益和效益；另一方面由于人们对高职教育认识的深化，提高质量已成为高职教育改革与发展的主旋律。作为培养高质量优秀人才的基本保证之一的教材建设摆上议事日程，教育部高教司在《关于加强高职高专教育教材建设的若干意见》中提出了“五年内编写出版一批有特色的基础课程和专业主干课程教材”的目标。仅就数学学科而言，五年来高职高专教材纷纷问世，仅高等教育出版社就有多套高职高专数学教材出版，其他如清华大学出版社、化学出版社等也有多套高职高专数学教材出版。
　　
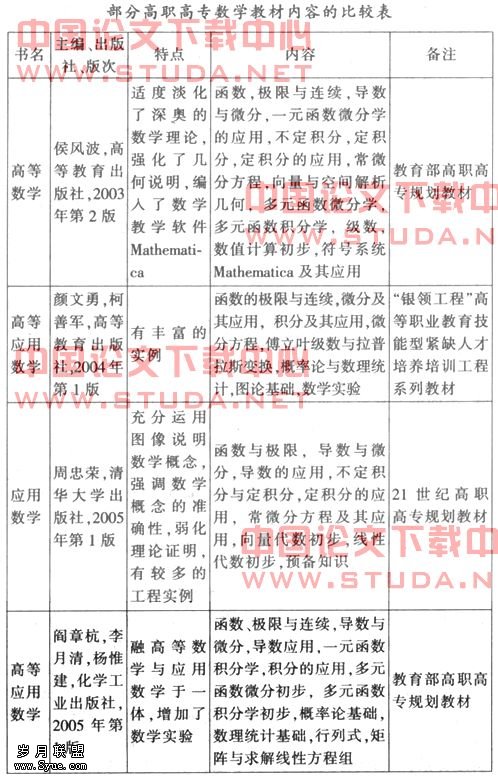
　　这些教材都是根据1999年教育部组织制定的《高职高专教育高等数学课程教学基本要求》和《高职高专教育专业人才培养目标及规格》编写的，总的来说，这些教材都在一定程度上体现了高职特色。但在教学实践中也发现一些问题，一是有的教材脱胎于普通高等院校的《高等数学》，保留了原有的学科理论体系，教材体系严谨，篇幅较长，需要学时较多，与当前高职高等数学课程总学时数趋于减少的情况不相适应，与当前高职学生来源不一、基础参差不齐与认知水平普遍较弱的情况不相适应。二是有的教材基于面向应用的考虑，在教材中大量引入专业性较强的实例，学生难以接受。本文拟结合参加编写高职教育应用型人才培养培训工程系列教材之一《微积分应用基础》（2006年6月高教版）的实际，谈谈高职高等数学教材编写的一些想法。
　　
　　确定的高职数学课程教学目标
　　
　　课程目标直接反映出课程的层次、规格和要求，是编写教材的依据。但目前人们对职业教育中的数学课程目标似乎清一色地廓定为“工具课”,笔者认为这样的认识是有欠缺的。高职数学课程目标应根据高职培养目标来确定。
　　1997年，联合国教科文组织公布的《国际标准分类法》（ISCED）中，将整个教育体系划分为七个层次。其中第五层次为高等教育第一阶段，包括专科、本科及硕士研究生学位课程。第五层次又明确地分为A、B两类，普通高等教育划为“5A”，高职教育划为“5B”。因此，高职教育属于高等教育，但又不同于普通高等教育。高职教育的显著特点是既有高等性又有职业性。教育部《关于加强高职高专人才培养工作的意见》指出：“高职高专培养拥护党的基本路线，适应生产、建设、管理、服务第一线需要的德、智、体、美等方面全面发展的高等技术应用型人才。”明确了高职教育的人才培养目标，高职教育是面向经济建设第一线，培养具有良好职业道德和敬业精神，具有必备的基础理论知识和专门知识，掌握高新技术应用并具有较强实践能力的实用型人才的大学专科层次的教育。
　　根据高职教育的培养目标，高职数学课程应具备工具功能，但同时也应具备思维训练与素质提高的功能：（1）了解数学概念产生的背景，理解概念的本质，掌握基本概念的几何解释、经济意义和物理意义等，体会其中所蕴含的数学思想和方法，会用有关概念、公式、定理解决实际问题，在数学应用中掌握基础知识和数学思想方法，为专业课的学习提供必要的数学基础。（2）提高学生的基本运算能力、基本工具的使用能力，达到会算、够用的目的。（3）将数学建模的思想和方法有机地贯穿于高等数学课程内容中，使学生在学习高等数学基础知识的同时，初步获得数学建模的知识和技能，提高学习数学的兴趣，形成科学的学习态度，培养学生的创新意识，为他们将来应用数学知识与方法研究和解决相关专业问题打下基础。
　　
　　以应用能力培养为主线设计知识应用结构体系
　　
　　传统的高等数学教材强调系统性，其内容结构基本上是按学科逻辑顺序编排的。高职数学教材不宜过多强调知识的系统性，而应加强职业针对性，突出应用性、实用性，加强数学应用不仅是在例题或习题中增加应用题，而应是在教材中贯穿应用意识。这方面可借鉴美国的整体数学教材，整体数学是2001年由美国迈克道格公司出版的一套数学教材，该教材有三个显著特点，一是以应用数学为主线，每节教学内容大体围绕两个应用性问题展开，教材中有关数学应用的例子和习题比比皆是，其内容涉及建筑、文化、商业、家庭理财、全球性问题（如粮食问题、人口问题、环境保护问题）给社会带来的影响和作用；二是教材抓住日常生活中的问题作为新内容的引入，常常围绕应用展开，这种引入方式不仅有利于创设问题情境，而且有利于使学生体会到数学就在身边；三是教材辟有应用栏目，如“聚焦职业”，就是专门介绍各行各业应用数学的事例的。
　　精选高职高等数学课程教学内容
　　
　　内容选取的适当与否在很大程度上决定着教材是否符合高职实际，是否具有高职特色。部文件指出：“基础理论教学要以应用为目的，以必需够用为度”，这个定位是符合我国高职教育实际的。“必需、够用”是针对“重理论轻实践”的弊端提出的，其目的是强调基础课要为专业课服务。人们往往对此有片面的理解，以为“必需”所指的范围或“够用”所指的深度，均应限于对专业课的要求。随着人们对高职教育认识的深化，“必需、够用”尽管仍可作为处理基础课与专业课的一个基本原则，但对其内涵应有一个全面、准确的理解，高职高等数学的内容不仅要选择专业课“必需”的数学知识，同时还要兼顾数学知识的相关性以及学生可持续的需要。高职高等数学内容应具有基础性、应用性、可接受性与性的特点。
　　注重知识衔接，力求平稳过渡我国高职院校的生源由高中生和“三校生”构成，数学基础参差不齐。一般而言，“三校生”的数学基础较高中毕业生要差些。因此，高职数学教材编写应切实注意不同生源的实际状况，充分研究中学数学教材、中专数学教材、职高数学教材与技校数学教材，注重衔接，保证不同来源的学生在学习高职数学时能够平稳过渡。
　　淡化理论体系，立足实际应用为专业课学习服务和培养学生运用数学知识解决实际问题的能力是高职数学教学的主要目标，因此，基础理论要以应用为目的，以“必需、够用”为度，以讲清概念、强化应用为重点，尽量淡化理论推导，尽量借助图形、实例解释验证，使抽象问题具体化、形象化。
　　改革课程内容，融入建模思想长期以来，数学课程已自成体系，教学围绕数学概念、方法和数学理论开展，处于自我封闭状态。即使传授了许多定理、公式和方法，仍免不了成为一堆僵死的教条，以至于学生在学了许多被认为是非常重要和有用的数学知识后，却不会应用或无法应用，甚至觉得除了应付之外毫无用处。数学建模为数学与实际问题的联系打开了一条通道，数学建模要求学生对实际问题中的数据信息加以整理、归纳、简化、抽象，并用数学语言表达出来，还要求学生对结论加以验证、完善、推广。数学建模有助于学生体验数学在解决实际问题中的价值和作用，体验数学与日常生活和其他学科的联系，体验综合运用数学知识和方法解决实际问题的过程，增强应用意识，有助于激发学生的学习兴趣，发展学生的创新意识和实践能力。由此可见，将数学建模的思想与方法融入高职高等数学课程内容中，对于提高高职生的数学应用能力，培养高职生的创新能力是非常必要的。数学建模主要可包括以下内容：（1）介绍数学建模的一般步骤与颇具普适性的数学建模方法。（2）选择一些贴近高职生认知水平、贴近高职生生活实际、涉及的专业知识不多又易于理解的案例。（3）数学软件的使用介绍。随着机与计算技术的发展,求解数学问题有了功能强大的数学软件（如Mathematica、Maple、Matlab等），利用数学软件的数值计算、符号运算与函数绘图等功能，可方便、快捷地进行画图与数值计算（包括求极限、求导数、求积分、求解微分方程、基本矩阵运算、解线性方程组等）。因此，高职数学教材应结合具体内容适时介绍数学软件的使用方法，提高学生利用数学软件分析处理实际问题的能力。
　　挖掘文化底蕴，加强人文教育数学并非一系列数学符号与技巧的堆砌，正如绘画不只是颜料的调配，不只是音符的组合一样，数学离不开人的情绪和动机，离不开人的情感和意志。克莱因曾说：“在最广泛的意义上说数学是一种精神，一种理性精神。正是这种精神，使得人类的思维得以运用到最完善的程度，亦正是这种精神，试图决定性地影响人类的物质、道德和社会生活；试图回答有关人类自身存在提出的问题；努力理解和控制；尽力去探求和确立已经获得知识的最完美的内涵。”因此，数学不应等同于数学知识的汇集，而应将其看成是人类的一种创造性的文化活动，学生学习数学绝非单纯为了获得相关的知识，更重要的是通过学习接受数学精神和其思想方法，将其内化成人的智慧，使思维能力得到提高，意志品质得到锻炼，并将其迁移到工作、学习和生活的各个方面。高职数学教材可适当介绍一些有关数学发现与数学史的知识，如某一概念的提出及演变过程，某一重要定理的背景，某一数学方法的发现及对数学乃至、及社会发展的推动作用，从而使学生明白，历史上人们为什么要研究某个问题。同时，可结合课程内容介绍一些数学家的生平、逸闻趣事、数学符号的由来、历史上利用数学知识成功解决问题的真实例子，使学生了解数学知识的产生与发展首先源于生活需要，体会数学在人类历史发展中的作用，激发学生学习数学的兴趣。例如，在“极限与连续”这一章可结合“无穷小”的概念介绍“第二次数学危机”的产生原因与解决过程；在“导数与微分”这一章，可介绍微积分创立的时代背景和历史意义，介绍微积分在航海、采矿、机械制造、水利、军事、天文等技术领域的广泛应用；在“微分方程”这一章，可介绍1991年海湾战争时，美国利用流体力学的基本方程以及热量传递的方程建立数学模型，解决了科威特的油井是否可以被全部烧掉的难题；在“概率与统计”这一章，可介绍概率论产生的背景（分赌本问题），“洛伦茨曲线”（反映收入差异的一种图形描述）等等。
　　
　　在内容的组织上突出模块化思想
　　
　　为了使一种教材适应相近专业或不同专业的教学需要,对课程内容作模块式处理是可取的。高职高等数学教材的内容应采用模块化组织，具有一定的可剪裁性和可拼接性。模块式教材既能适应学制缩短、课时减少的实际状况，又可以根据行业岗位（群）对知识的需求，选取最适用的内容进行教学。一元函数微积分是高职院校各专业的共同需求，这部分内容可作为基础模块，其他内容如常微分方程、向量代数与空间解析几何、多元函数微积分、无穷级数、线性代数、线性规划、图论、概率统计等，不同的专业有不同的需求，这部分内容可作为专业模块，供不同专业选用。如机类专业可选择向量代数与空间解析几何、多元微积分，电类专业可选择线性代数、级数、图论、多元函数微积分，经济与管理类专业可选择线性代数、线性规划、概率统计、图论等。另外，考虑到我国高职院校生源多样性的特点，还应设置预备知识模块。
　　
　　以“问题情境—展现知识—实现应用”的思路开展教学
　　
　　数学是现实的，学生从现实生活中学习数学，再把学到的数学知识应用到现实中去，这是数学教育的必然趋势。学生的数学能力不仅表现在掌握了多少数学知识，更在于是否具备运用数学知识解决实际问题的能力。教育心研究表明，当学习的材料与学生已有的知识和生活经验相联系时，可以使学生对数学产生亲近感，激发学生学习数学的热情。因此，高职数学教材应以“问题情境—展现知识—实现应用”的思路呈现教学内容。如数学概念的引入要力求从实际问题出发，突出问题的实际背景，以引例方式呈现。为了强调数学理论的实用性，突出运用数学的方法，在给出数学的一般性结论后，应尽量提出一些更具体的应用问题，并以案例方式呈现。涉及人们生活中衣、食、住、行的各种现实问题以及经济活动、运输过程、人口控制、环境保护、资源开发、科学管理等诸方面的实际问题与专业问题都是较为理想的选择，为了兼顾不同专业的需要，同一内容应有结合不同专业实际的多个案例以备选用。
　　
　　：
　　[1]黄克孝.职业和技术教育课程概论[M].上海：华东师范大学出版社，2001.
　　[2]朱春浩.以应用能力培养为主线，建立高职数学课程体系[J].职业技术教育（教科版），2001，（4）．
　　[3]曾庆柏.中高等职业教育数学课程改革的探索[J].职业技术教育，2005，（4）．
　　[4]何友义.高职教育教材建设的思考[J].中国高教研究，2002，（11）．
　　[5]杨赛.从数学的广泛应用性角度谈高中数学教材的编写[J].课程·教材·教法，2000，（3）．