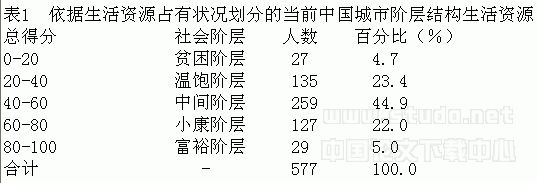
完美风暴预言的评价（一）

　　关键词：灰色系统　主成份分析法　BP神经

　　论文摘要：英国家约翰·贝丁顿于 3 月 18 日在英国《卫报》发表文章称，气候变化和人口增长将导致食品、水和能源短缺，进而引发大规模移民、公共骚乱和国际冲突。如果未来数年内没有充分准备的话，到 2030 年，世界将面临“完美风暴”，出现大的动荡。为了评价和印证约翰·贝丁顿的预言我们建立数学模型进行了对预言的评价，这对人们有警示和的现实意义。

　　对于人口的增长问题，我们分别用logsitic阻滞增长模型和灰色系统模型进行了预测分析，结果表明logistic阻滞增长模型得出的结论与约翰·贝丁的预测符合较好，得出 ，2020年世界人口预测将达到80.86亿。由一些有效数据，建立合理的灰色系统模型对未来的2030年粮食储存量进行推算，得出2030年的粮食储存量，从而论证了约翰．贝丁顿提出的观点是科学的。能源问题我们建立了灰色系统模型进行了分析，结果得出是。

　　得出个个子模型关系后再采用主成份分析法，得出最终的贡献率，个个变量因子对于结果的贡献率。然后用BP神经网络综合分析了完美风暴。

　　在2030年，资源和粮食都同时短缺，也就是说按现在这个程度在2030年将发生食品、水和能源短缺，如果未来数年内没有充分准备的话，到 2030 年，世界将面临“完美风暴”，出现大的动荡。人口的持续增长将会在未来 20 年里引发对食品、水和能源的大量需求，与此同时，各国政府还必须应对气候变化。所有这一切都将同时到来。据贝丁顿教授说，再过 20 多年，全球人口将增加到大约 83 亿。仅此一点，就意味着全球资源需求将在未来变得更大。贝丁顿博士警告说，资源短缺压力将急剧增加，气候变化将使问题恶化。目前，全球的粮食储存量太小，只有年消费量的 14%，一旦发生干旱或者洪灾，粮食就会严重短缺。他说：“我们的粮食储备是 50 年来最低的，到 2030 年，我们对粮食的需求会增加 50%，同时，我们对能源的需求也会增加 50%，淡水的需求会增加 30%。”我们的创新之处在于：一.利用灰色系统进行了对世界人口的预测。二.利用主成份分析法给出了个个变量之间的关系。三. 运用BP神经网络进行了对于完美风暴的预测。

　　一.问题的重述

　　贝丁顿说，人口的持续增长将会在未来 20 年里引发对食品、水和能源的大量需求，与此同时，各国政府还必须应对气候变化。所有这一切都将同时到来。据贝丁顿教授说，再过 20 多年，全球人口将增加到大约 83 亿。仅此一点，就意味着全球资源需求将在未来变得更大。贝丁顿博士警告说，资源短缺压力将急剧增加，气候变化将使问题恶化。目前，全球的粮食储存量太小，只有年消费量的 14%，一旦发生干旱或者洪灾，粮食就会严重短缺。他说：“我们的粮食储备是 50 年来最低的，到 2030 年，我们对粮食的需求会增加 50%，同时，我们对能源的需求也会增加 50%，淡水的需求会增加 30%。”

　　21世纪是人类发展最快的时期，也是我们引领世界的辉煌时期。 近几年来，科学技术的迅猛发展加速了人类文明的繁荣。同时亦增强了人类对环境的影响能力，引起了全球各种问题出现了突出的矛盾，成为社会最严重的挑战。正如英国科学家约翰．贝丁顿于3月18日所说，由于气候变化和人口增长将导致食品、水和能源短缺，从而引发大规模移民、公共骚乱和国际冲突，最终在2003年造成“完美风暴”的发生。并且，约翰．贝丁顿也提出，我们的粮食储备是50年来最低的，到2030年，我们对粮食的需求会增加50％，同时，我们对能源的需求也会增加50％，淡水的需求会增加30％，问题由此而生，约翰．贝丁顿提出的观点是否科学，我们有必要根据资料对此观点进行验证。我们以人口与粮食的关系为重点进行论述，假如，到2030年，我们对粮食的需求会增加50％。则在人口随着年份的增加而按照阻滞增长模型进行增长，同时在每年粮食总量不变下，粮食贮存量的变化和粮食消费量的变化建立三者的关系。

　　二．问题的分析

　　2.1对问题背景的分析
　　如今，由于气候的变化以及人口的迅速增长使得食品、水和能源的短缺，并且人类的生活环境变得更加恶劣，如果长此以往，战乱与国际冲突，将随时可能爆发，人类的生存面临这巨大的挑战。所以，对现在人类生活环境状况的评估是非常具有必要性的，同时对于人口增长、能源、粮食和淡水的需求预测也是很有必要的，因为只有做好了，预测分析工作，才能够对未来的发展趋势由很好的了解，对与制定补救措施具有很大的帮助。

　　2.2对约翰· 贝丁顿观点的论证分析
　　对于文中约翰· 贝丁顿所提到的，人口、能源、粮食和淡水需求量到2030年会发生重大变化。为了来论证这一观点的正确性，首先就是搜集相关的数据，然后利用相关的模型对上述四个因子分别进行预测。通过模型所得到的预测值来判定约翰· 贝丁顿观点的正确性。

　　2.3对人口、能源、粮食、淡水之间关系的分析

　　研究人口、能源、粮食、淡水之间关系的意义在于对运用于人类生存危机状况量化处理的模糊综合估计方法中权值矩阵的确定起到关键作用，所以，通过利用主成分分析法可以求出四者之间的相关性，并且通过相关性可以构建四者之间的函数关系。

　　2.4对“完美风暴”危机预测模型的分析

　　人类生存环境的危机状况是一个抽象的概念，没有具体数值来表示。那么，对于这种情况，我们必须找到一种方法，使这种危机的状况能够被量化，于是我们选择用风险度来描述风险和时间的关系。

　　在得到每一年的危机状况的估计量化值（模型中我们称为危险评判参数）后，我们可以通过构建世界人口、能源、粮食和淡水需求量这四个因子与所求得的量化值之间的关系，于是利用BP神经网络来构建两者之间的输入输出关系，并且通过BP神经网络的网络训练模拟功能，可以预测出2030年人类生存环境的危机状况，以此进行判断“完美风暴”发生的可能性。

　　三.模型的建立以及求解

　　I.主成分分析法分析完美风暴一．世界人口增长的预测

　　3.1 logistic阻滞增长模型预测世界人口

　　3.1.1模型的准备

　　表3.1.1 世界人口随时间变化

1970至2006年世界人口统计（单位：万人）

1970至2006年世界人口统计（单位：万人）
年份	人口（万人）
1990	528500
1991	538500
1992	548000
1993	557200
1994	562980
1995	571606
1996	574560
1997	584590
1998	589848
1999	597773
2000	605412
2001	613010
2002	619973
2003	627252
2004	636969
2005	644598
2006	651776

图3.1.1世界人口随时间变化

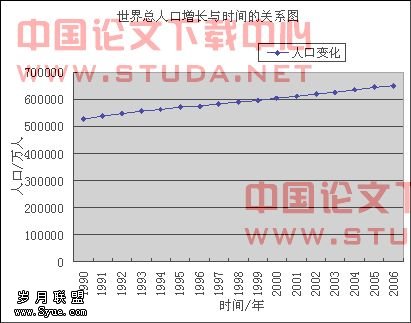
　　用EXCEL可以画出以上图形，虽然看起来是线性的，是由于纵坐标取值比较大的缘故，实际上并非是线性的，并且是符合logistic阻滞增长增长模型的。

  表3.1.1b近几年世界总人口情况

年份	年总人口数(亿)	出生率(%)	死亡率(%)	自然增长率(%)
1991	53.84	27	9	1.7
1992	54.2	26	9	1.7
1993	55.06	26	9	1.6
1994	56.07	25	9	1.6
1995	57.02	24	9	1.5
1996	57.71	24	9	1.5
1997	58.4	24	9	1.5
1998	59.26	23	9	1.4
1999	59.82	23	9	1.4
2000	60.67	22	9	1.4
2001	61.37	22	9	1.3
2002	62.15	21	9	1.3
2003	63.14	22	9	1.3
2004	63.96	21	9	1.3

　　3.1.2模型的假设

　　（1）世界人口的增长符合logistic阻滞增长模型，可以用此模型求解.

　　3.1.3logistic阻滞增长模型的建立以及求解

　　于是有：

                            （1）

　　对 的一个最简单的假定是，设 为 的线性函数，即

                                （2）

　　设自然资源和环境条件所能容纳的最大人口数量，当时人口不再增长，即增长率，代入（2-2）式得，于是（2-2）式为

                                  （3）

　　将（2-3）代入方程（2-1）得：

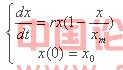                                                      （4）

　　解方程（2-4）可得：

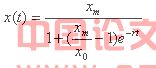                          （5）

　　3.1.3模型的求解

　　为了对以后一定时期内的世界人口数做出预测，我们首先从世界银行数据库上查到世界人口从1990年到2007年部分年份总人口的数据

　　（1）将1990年看成初始时刻即 ，则1991为 ，以次类推，以2007年为t=7作为终时刻。用函数（5）对表3.1.1中的数据进行非线性拟合，运用Matlab编程得到相关的参数 ，可以算出可决系数（可决系数是判别曲线拟合效果的一个指标）：

　　

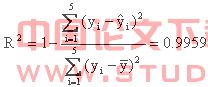
　　可以算出可决系数 得世界部分年份人口变化趋势的另一拟合曲线：

                （2-7）

　　进行预测得（单位：千万）：

　　 X(20)=80.86

表3.1.3  各年份世界总人口用不同拟合曲线预测数（单位：亿）

　　由上表可以看出：在2020年总人口就已经超过了80.86亿,比较接近的预测。

　　3.1.4型的误差检验

　　在估计阻滞增长模型的参数时没有用到2000年的实际数据，是为了用它做模型检验。我们用模型的2007年世界人口总数与已知的实际数据相比较，来检验模型是否合适。

 

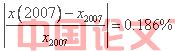
　　经计算，误差仅为0.0186%，故可以认为该模型的精度是很高的。

　　其中算法及程序见附录

　　3.2 灰色系统模型预测世界人口

　　灰色系统理论的微分方程为GM模型，GM(1，1)表示1阶，1个变量的微分方程模型.

　　记原始数据序列/* MERGEFORMAT 如下：

 /* MERGEFORMAT 

　　它的时间响应序列为：

                           /* MERGEFORMAT                      

　　其中， /* MERGEFORMAT

　　即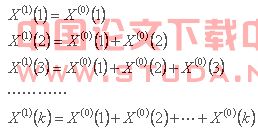： /* MERGEFORMAT                                  

　　因此通过计算得：表3  /* MERGEFORMAT 的值

/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
53.84	108.04	163.1	219.17	276.19	333.9	392.3
/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
451.56	511.38	572.05	633.42	695.57	758.71	822.67

　　然后计算/* MERGEFORMAT 的紧邻均值生成序列/* MERGEFORMAT

  　　 /* MERGEFORMAT                      

　　其中，/* MERGEFORMAT

　　得到：表4 /* MERGEFORMAT 的值

/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
53.84	80.94	135.57	191.135	247.68	305.045	363.1
/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
421.93	481.47	541.715	602.735	664.495	727.14	790.69

　　我们称方程 /* MERGEFORMAT 为灰色GM(1，1)模型，其中/* MERGEFORMAT 是需要通过建模求解的参数，若 /* MERGEFORMAT 为参数数列，且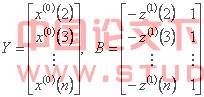/* MERGEFORMAT        其中  /* MERGEFORMAT

 /* MERGEFORMAT 则求微分方程/* MERGEFORMAT 的最小二乘估计系数列，满足

 /* MERGEFORMAT                           

　　称 /* MERGEFORMAT/* MERGEFORMAT 为灰微分方程，/* MERGEFORMAT 的白化方程，也叫影子方程.

　　因此，根据上述所说则有

　　1.白化方程/* MERGEFORMAT 的解或称时间响应函数为 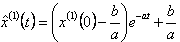/* MERGEFORMAT          

　　2.GM(1，1)灰微分方程/* MERGEFORMAT 的时间响应序列为 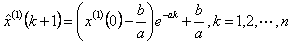/* MERGEFORMAT                                    

　　3.取/* MERGEFORMAT ，则 /* MERGEFORMAT                                    

　　4.还原值

              /* MERGEFORMAT                   

　　根据方程对参数的/* MERGEFORMAT 作最小二乘估计，得

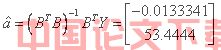                   /* MERGEFORMAT                          (21)

　　设 /* MERGEFORMAT

　　由于 /* MERGEFORMAT ，可得GM(1，1)模型的白化方程为

                     /* MERGEFORMAT                       (22)

　　它的时间响应式为

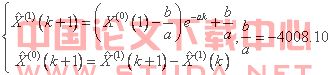                /* MERGEFORMAT              

　　由此得模拟序列

                       /* MERGEFORMAT                  

　　相应的值为：/* MERGEFORMAT 的值

/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
53.84	54.52	55.25	56.00	56.75	57.51	58.28
/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
59.07	59.86	60.66	61.48	62.30	63.14	63.99

　　灰色系统模型的检验

　　定义1.设原始序列

      /* MERGEFORMAT               

　　相应的模型模拟序列为：

             /* MERGEFORMAT                   

　　残差序列：

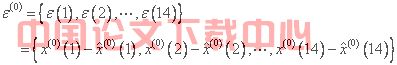              /* MERGEFORMAT        

　　相对误差序列：

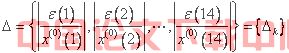　　 /* MERGEFORMAT                       

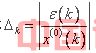　　1.对于/* MERGEFORMAT ，称/* MERGEFORMAT 为k点模拟相对误差，称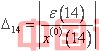/* MERGEFORMAT 为滤波相对误差，称/* MERGEFORMAT 为平均模拟相对误差；

　　2.称 /* MERGEFORMAT 为平均相对精度，/* MERGEFORMAT 为滤波精度；

　　3.给定/* MERGEFORMAT ，当 /* MERGEFORMAT 成立时，称模型为残差合格模型.

　　定义2 设/* MERGEFORMAT 为原始序列，/* MERGEFORMAT 为相应的模拟误差序列， /* MERGEFORMAT 的绝对关联度，若对于给定的/* MERGEFORMAT ，则称模型为关联合格模型.

　　定义3 设/* MERGEFORMAT 为原始序列，/* MERGEFORMAT 为相应的模拟误差序列，/* MERGEFORMAT 为残差序列.

 /* MERGEFORMAT 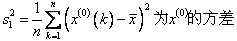      /* MERGEFORMAT

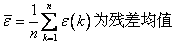 /* MERGEFORMAT  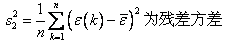        /* MERGEFORMAT

　　1.称/* MERGEFORMAT 为均方差比值；对于给定的/* MERGEFORMAT ，当/* MERGEFORMAT 时，称模型为均方差比合格模型.

　　2.称/* MERGEFORMAT 为小误差概率，对于给定的/* MERGEFORMAT ，当/* MERGEFORMAT 时，称模型为小概率模型合格模型.

表3.2.1精度检验登记参照表

精度等级	相对误差	关联度	均方差比值	小误差概率
一级	0.01	0.9	0.35	0.95
二级	0.05	0.8	0.5	0.8
三级	0.1	0.7	0.65	0.7
四级	0.2	0.6	0.8	0.6

　　由已知数据我们算出的结果为

表 3.2.2残差序列

/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
0	-0.32	-0.19	0.07	0.27	0.20	0.12
/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT	/* MERGEFORMAT
0.09	-0.04	0.07	-0.11	-0.15	0	-0.03

 /* MERGEFORMAT 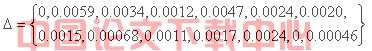 /* MERGEFORMAT

　　计算得平均相对误差： /* MERGEFORMAT

　　模拟误差：/* MERGEFORMAT .精度为一级

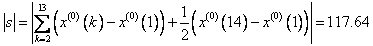　　计算/* MERGEFORMAT 与/* MERGEFORMAT 的灰色关联度 /* MERGEFORMAT

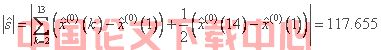              /* MERGEFORMAT                 

             /* MERGEFORMAT                

  /* MERGEFORMAT

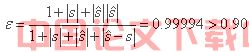                       /* MERGEFORMAT                               

　　精度为一级

　　计算均方差比

　　  /* MERGEFORM AT                   

　　 /* MERGEFORMAT                            

　　 /* MERGEFORMAT

            

　　/* MERGEFORMAT                              

　　 /* MERGEFORMAT

　　所以，由/* MERGEFORMAT 均方差比值为一级计算小误差概率

　　由/* MERGEFORMAT