岁月论坛

当前位置：首页 > 论文 > 社会 > 社会其它相关

完美风暴预言的评价（三）

来源：岁月联盟作者：李占海时间：2010-08-12

　　 ----输入层到隐含层的权值；

　　 ----隐含层到输出层的权值；　

　　 ----隐含层的阈值；

　　 ----输出层的阈值；

　　该模型可用图直观表示如下：

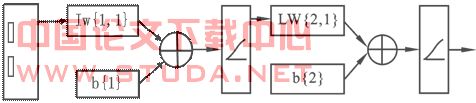
　　得到的神经的权值矩阵请具体附录6

　　四．模型结果及其分析

　　一.关于主成分分析法结果的分析

　　1.对于人口的预测两个模型得出的结果都比较合理，和约翰提出的相吻合，得出80.86的值。

　2.对于能源，水资源的预测也较为标准。

　3.得出了个个因子对于果的贡献率，结果在2030年发生完美风暴。

　　二.关于BP神经网络结果的分析

　　得出的结果也和约翰的预言一样，将在2030年完胜完美风暴。

　　三．.对2030年“完美风暴”进行预测结果

通过上述模型的构建，我们已经对1987至2002年十六年的世界人口、能源需求量、粮食需求量、淡水需求量的统计样本与危险评判等级参数之间的关系进行了神经网络的训练，得到了能够反应两者之间的关系（是一个复杂的网络结构，通过权值矩阵来表示特征），若对“完美风暴”进行预测，只要将2030年所预测的世界人口、能源需求量、粮食需求量、淡水需求量的值输入神经网络中，就会输出相应的危险评判等级参数，于是根据参数就可以判断“完美风暴”发生的可能性。

　　经上述工作，我们得到了2030年世界人口、能源需求量、粮食需求量、淡水需求量的预测样本如下：

世界人口（万人）	能源需求（标准油：万桶）	粮食需求（万吨）	淡水需求（亿立方米）
931070	121412	25944	152137

通过神经网络模型的模拟训练的到以下五个危险评判等级参数：

表5.8 2030年危险评判等级参数


19.6700	13.6741	15.4244	24.5720	26.9043

四.对能源、粮食、淡水需求量、世界人口预测值的分析
　　通过各种模型我们预测出2030年世界人口、能源、粮食、淡水需求量的预测值，并且我们将以2006年的数据作为人类生活环境的现状。

表1人类生活现状与预测值对比

年份	2006	2030
世界人口（万人）	651776	931070
能源需求量（标准油，万桶）	83719	121412
粮食需求量（万吨）	17770	25944
淡水需求量（亿立方米）	96452	152137

　　通过上表的数据我们可以得到以下结果：

　　（1）世界人口达到93亿，远远超过83亿

　　（2）能源需求量增加45.09%

　　（3）粮食需求增加45.9%

　　（4）淡水增加57.7%

　　根据上面四个结果，初步论证了约翰• 贝丁顿的“完美风暴”理论的正确性。

　　五．对BP神经网络的“完美风暴”预测值的分析

　　通过神经网络的模拟可以得到2030年的危险评估等级参数，将表5.8与表5.7.1的比较不难发现，到2030年，人类生存系统的危险评估等级参数非常高，达到危险的级别，证明了“完美风暴”发生的可能性非常大。并且我们也预测出2030年至2040年的危险评估等级参数，得出随着时间的不断推移，“完美风暴”发生的可能性越来越大，人类生存的环境将变得更加危险、恶劣，结果如下：


2031	19.7421	12.2322	24.3235	23.4214	11.3444
2032	21.4323	21.2445	13.4326	21.4313	21.3254
2033	24.0521	28.6923	26.9076	28.8943	28.3772
2034	25.4890	28.0485	28.9985	20.4787	29.8473
2035	29.0982	29.7872	29.0785	20.8893	29.9746
2036	30.8741	34.8983	38.7658	32.8989	33.6786
2037	38.6482	38.9874	38.6985	30.9875	39.8786
2038	39.8185	35.7623	40.8392	38.8899	45.2989
2039	43.8972	42.9824	32.0835	41.9782	41.8974
2040	48.9878	49.7864	48.7676	44.4896	35.3254

　　六..对BP神经网络的稳定性分析

　　鉴于模型的目的是为了预测，所以模型的稳定性显得尤为重要，必须对模型进行稳定性分析。

　　BP算法是一个有效的算法，由于具有理论依据坚实、推导过程严谨、物理概念清晰和通用性好等特点，是当前网络学习的主要算法。同时存在一些不足，主要有：训练时间长，出现局部极小值，网络结构难以确定等。本文在建立神经网络模型过程中，通过预处理以及合理选择训练方法实现网络收敛、避开局部极小值，有效地提高了模型的稳定性。

　　（1）数据正规化处理（归一化）和Matlab工具箱函数prestd实现数据正规化，通过对样本集数据参数和输出样本数据参数进行正规化处理，可有效防止网络训练进入局部误差最小或误差震荡缺陷[14]；

　　（2）根据进行设计隐含层节点数，有效设计网络，保证训练精度、减少训练复杂度、缩短训练时间

　　（3）考虑到数据样本的随机性和非线性性，采用对非线性问题解决较好的S型传输函数。S传输函数使得输出值在0和1之间，使算法收敛速度加快，对每次训练进行有效调整，达到加速收敛目的；

　　（4）倾向于选取较小的学习速率以保证系统的稳定性,学习速率的选取范围一般在0. 01～0. 9之间。我们选择网络学习速率为0. 05 。

　　（5）采用traingdx训练函数训练，附加动量法使反向传播减少了网络在误差表面陷入低谷的可能性有助于减少训练时间。

　　综上所述，本文建立的神经网络模型通过合理的处理和有效的方法选取，确保BP网络高精度快速收敛。确保预测模型的精度和健壮性。

五.模型的优缺点分析

　　模型的优点：

　　1、运用灰色预测模型它能够根据数据的变化，较准确的预测数据.得出的数据有一定的准确度，并且模型检验好.

　　2、在此基础上由于是对较长时间的预测，为了保证模型的稳定性，我们又运用了离散型的灰色预测模型，它能保证模型具有很好的稳定性，对于长期的预测也会较准确.

　　3、运用微分方程模型，在已知增长率的情况下，能很好的预测在将来人口等因素的变化，有很好的稳定性和准确性.

　　4、本文所用数据来自联合国统计局、世界年鉴和世界统计年鉴，具有很强的真实性与代表性；

　　5、本文在建立了基于主成分分析法的危机预测模型，将危机发生的标准进行了量化处理；

　　6、本文在预测人口增长时使用了组合预测模型，大大提高了模型的预测精度；

　　7、本文将原模糊问题具体划分为若干问题，文章的思路清晰且具有很好的连贯性。

　　模型的缺点：

　　1.在建立危机预测模型时没有完全考虑到所有的因素；

　　2.在考虑环境与气候因素的影响时，只做出了定性的分析。

　　3.由于对较长时间的分析预测加上数据来源可能的不准确性，导致算出来的误差增加；对于问题原因的讨论不全面导致遗漏有些因素或者我们假设时忽略了一些因素，也可能造成误差的增大.

　　总之，该模型实用性较强，可以印证约翰提出的论断。

六．模型的改进方向

　　1.在主成分分析时增加变量因子，全面考虑，量化题目中给出的个个函数及其参数。

　　2.在算结果时对结果进行人为的修正。

七.写给有关政府部门的报告

　　（一）能源可持续

　　1.当今能源的现状

　　1994年末全球的一次能源的可采储量为14277.34一吨标煤，其中煤占73.1%，石油占13.8%，天然气占13.1%，而当年的开采量为104.481亿吨标煤。静态储采比137年，即经过137年后，一次性能源将被开采完全。这绝不是危言耸听，而是铁一样的事实，即使科技的进步使我们的开采技术提高，但是那也只是推迟期限，能源枯竭终究会到来，对此我们该怎么办呢？要想从本质上解决能源问题，就要从能源的本身入手，积极开发新型能，就是一种有效而长远的方法。风能，太阳能，地热能，潮汐能，生物质能源都是新兴的清洁可再生能源，各国要努力在这方面投资开发，使之形成产业化。比如在地区，利用秸秆和畜禽粪便发展沼气，具有广阔的前景。

　　2.提高公民的节能意识

　　公民的节能意识在解决能源问题中同样扮演着重要的角色，在这方面挪威的方法就很值得借鉴。在挪威政府把增强公众的节能意识作为可持续发展的重要一环。在书店及公共图书馆里常年摆放着各种免费的环保方面的宣传资料，在中小学的教科书里也增加了相应的环境能源保护部分，政府还出台一系列政策加强的节能意识。

　　3.加强国际之间的合作

　　21世纪，世界各国更加重视发展，事实早已表明，任何国家没有发展就没有前途。发展需要能源，而世界常规能源并不是取之不尽，用之不竭的。发展的迫切要求和能源的匮乏已经不只是某些国家的问题了，世界各国都必须面对能源短缺的现实。当前国际油价居高不下是世界各国所面临的严峻挑战，所以一方面需要各国在能源方面做出开源节流的努力，另一方面也需要积极扩展新的发展思路，开展国际之间的对话，彼此增强了解，广泛合作，才能有利于解决国际能源问题。

　　4.开发新的能源技术

　　当今最新的，也是发展最成熟，最有前景的新能源就是核能。核能发电对环境的污染小，经济效益高。目前发展比较好的是核裂变发电，但是尽管能源潜力大，由于其具有放射性，且发电原料在地球上很稀少，且提纯困难，所以虽然被广泛使用，但是必将被另一种核能替代，那就是核聚变。核聚变无污染，且原材料非常丰富，所以被人们认为是人类最有希望的能源。

　　人类的文明是建筑在对于能源的认识和掌握上的，每一次人类文明的跨越都与能源技术的进步密不可分。因此要实现可持续发展，世界必须进行一次能源革命，这不仅是技术上的一次革命，能够使世界的能源系统持续保证经济的发展和社会进步；同时也是观念上的一次革命，需要我们树立“发展观”

　　建立一个新的能源体系，使可持续发展化为全社会的动力和目标，是和谐社会成为我们永远赖以生存的环境。

　　（二）粮食可持续发展

　　认真确立以农业为基础，始终坚持不放松粮食生产的基本思想解决粮食问题，其中的一个有效途径是提高粮食的产量。可以通过稳定粮食的播种面积，挖掘潜力，扩田增粮。俗话说“皮之不存，毛将焉附”，有田才有粮，所以全世界范围内一定要保证种粮面积，但是这并不等于是无节制的开发，向在某些地区依然存在的刀耕火种现象依然存在，这威胁的就不只是人类的嘴巴问题，更切身的是关系到人类长久生存的权利。

　　2.加大科研资金的投入

　　全世界都要改变粮食生产的模式，要有原来的规模效益向节约型、集约型转变，努力提高粮食的产量，积极做到科技兴农。一方面可以加大科研经费的投入，另一方面要鼓励农业科技人员到粮食生产的第一线，进行技术指导，加强农、科、教的紧密结合，扶持种粮能手和种粮大户，提高农民科技水平等等。另外，在整个世界要积极推进农业机械化，多采用大规模农场式的收中，努力提高集团效益。

　　3.加大农产品的流通机制

　　现在在世界的好多地方，出现着这样的问题，就是农民的生产往往不能提供社会所需，设置有时候是背道而驰的。面对这个问题，各国政府一定要加大农产品的流通体制改革，引导农民按市场规律调整农村经济结构，种植结构，养殖结构等等。政府要加强对市场的价格的调控能力，提高抵御市场风险的功能。只有农民这个粮食的原产者掌握好的方向，整个社会的粮食问题就走在了一条正确的道路上。

　　总之，最重要的是保护和合理开发利用资源，防止掠夺式、破坏性和浪费型的发展方式。保护和开发并重。建立适应社会市场的农业发展机制，世界的粮食可持续发展就有了希望。

　　（三）水的可持续发展

　　水是生命的源泉，但是地球上的淡水资源却极为的有限。地球上有70.8%的面积被水所覆盖，但其中的97.5%是咸水。余下的淡水中却只有87%是人类暂时难以利用的两极冰盖、高山冰川和高原地带的冰雪。因此，人类真正能够利用的水仅占地球总水量的0.26%。

　　目前，水资源短缺问题相当的严重，世界上有80多个国家约15亿人面临着缺水的威胁，其中26个国家的3亿多人完全生活在缺水的状态中，并且这一趋势人在加剧。预计到2010年的缺水国将增加到34个。

　　此外，水污染，水浪费等水环境危机更是加大了水短缺问题。部分国家经常遭受干旱、水资源短缺、地下水位下降，荒漠化逐渐扩大。

　　八．参考

　　【1】李静萍，谢邦昌，多元统计分析[M]，北京：人民大学出版社，2008

　　【2】安维默，王吉利，统计电算化[M]，北京：中国统计出版社，2000

　　【3】黄勇安，李文成，高小科：Matlab7.0/Simulink6.0应用实例仿真与高效算法开发[M]，北京：清华大学出版社2008

　　【4】龚沛曾等C/C++程序设计教程[M] 上海：同济大学出版社 2004

　　【5】李茜，王丰效，李晓静，多变量灰色预测模型的matlab程序，福建电脑，卷期号：32-48，2007年11期；

　　【6】魏一鸣，范英，韩智勇，中国能源报告(2006)战略与政策研究[M].北京：科学出版社，2006

　　【7】张　帆，俞奇勇，基于GM 的能源消费量坡度优化预测模型，水电能源科学，第25卷第3期，116-220，2007

　　【8】刘勇白林，《基于的回归分析模型在经济预测分析中的应用》，《中国管理信息化》，第11卷第15期，第66页～第67页

　　【9】刘志平石林英，《最小二乘法原理及其MATLAB实现》，《中国西部科技》，第17卷第17期，第33页～第34页

　　【10】姜启源谢金星叶俊等，《数学模型（第三版）》[M]，北京：高等出版社，2007

　　【11】刘思峰谢乃明，《灰色系统理论及其应用》[M]，北京：科学出版社

九．附录

1.matlab程序实现人口预测参量的求解

>>a [52.85 57.16 60.54 64.45] ; % 在此只取几值，然后求其平均值

>>t[0 5 10 15];

M文件代码如下：

X=52.85;

a= [52.85 57.16 60.54 64.45];

For j=1:1:5

i=14:15

M(i)=exp(-i):;

[xm,r]=solve[’ a(i)=xm/(1+(xm/52.85-1)* M(i)^r)’, ’ a(i+1)=xm/(1+(xm/52.85-1)* M(j+1))^r’];

t=1:1:30;

y=xm/(1+(xm/52.85-1)*exp((-r)*n));

plot(t,y,’b’t,a’ro’)

2.c++程序实现人口预测

#include "iostream.h"

#include "math.h"

#define N 30 // 定义符号变量以提高程序的普遍应用性

double peoplenumber(int n) //定义人口预测函数

{double x;

x=180.987/(1+(180.987/52.85-1)*exp((-0.0336)*n)); //预测函数

return x;

}

void main()

{int i,j(0);

double p[N];

for( i=0;i

{j=j+1;

p[i]= peoplenumber(j);} //预测人口数存入数组，调用人口预测函数

cout<<"人口预测logistic阻滞增长模型预测结果："<

for(i=9;i

cout<<"第"<

}

得出的结果：

备注：预测结果（单位是亿）

3.、1970~2006年世界人口统计数据（单位：万人）
年份	人口（万人）
1990	528500
1991	538500
1992	548000
1993	557200
1994	562980
1995	571606
1996	574560
1997	584590
1998	589848
1999	597773
2000	605412
2001	613010
2002	619973
2003	627252
2004	636969
2005	644598
2006	651776

4、1965~2006年世界能源需求量（标准油，单位：万桶）
年份			能源需求量
1990			66830
1991			66811
1992			67519
1993			67377
1994			68666
1995			69830
1996			71489
1997			73591
1998			73928
1999			75549
2000			76280
2001			76828
2002			77737
2003			79158
2004			81898
2005			83080
2006			83719

5、1987~2006年世界粮食需求量（单位：万吨）
年份		粮食需求量
1990		16542
1991		16608
1992		16683
1993		16754
1994		16824
1995		16850
1996		16910
1997		16928
1998		16930
1999		16973
2000		17118
2001		17230
2002		17492
2003		17460
2004		17495
2005		17573
2006		17770
6、1975~2006年世界淡水需求量（单位：立方米）
年份		淡水需求量
1990		39387
1991		39712
1992		40245
1993		41012
1994		43021
1995		46012
1996		50234
1997		55743
1998		61081
1999		65279
2000		70523
2001		74533
2002		78674
2003		83423
2004		87654
2005		91987
2006		96452

7.基于灰色理论的区间预测模型的在MATLAB上的实码：

%区间拟合函数求解

%拟合上函数

format long

x=[1 3 5 7];

y=[172430 175180 177670 183650];

f=@(a,x)(172430-a(1)/a(2))*exp(-a(2)*x)+a(1)/a(2);

[xx,res]=lsqcurvefit(f,[1,1],x,y) %结果数据 -7.51166737366709*10^3 -0.00004916823135*10^3

y1=(172430-149720)*exp(0.05111*x)+149720

plot(x,y1)

%区间拟合下函数

x=[2 6 11];

y2=[172220 176380 187640]

f=@(a,x)(172220-a(1)/a(2))*exp(-a(2)*x)+a(1)/a(2);

[xx,res]=lsqcurvefit(f,[1,1],x,y2) %结果数据 -7.51166737366709*10^3 -0.00004916823135*10^3

x=[1:12]

y2=(172220-152775)*exp(0.04917*x)+152775;

plot(x,y2)

%样本观察

x=[1:12];

y=[172430 172220 175180 175980 177670 176380 183650 184180 184950 187640 187640 189369];

y1=(172430-149720)*exp(0.05111*x)+149720;

y2=(172220-152775)*exp(0.04917*x)+152775;

plot(x,y,x,y1,x,y2)

%预测总趋势

x=[1:40]

y1=(172430-149720)*exp(0.05111*x)+149720;

y2=(172220-152775)*exp(0.04917*x)+152775;

plot(x,y1,x,y2)

jieguo=(y1+y2)/2

%结果：

(308453-197632)/197632

ans =

0.56074421146373

%预测结果

(7.5265-5.5502)/5.5502

ans =

0.3561

8.归一化后的神经训练样本

1	0.0952	0.0452
1	0.0971	0.0456
1	0.0977	0.0449
1	0.0962	0.0446
1	0.0957	0.0443
1	0.0937	0.0443
1	0.0949	0.0449
1	0.0955	0.048
1	0.0979	0.0526
1	0.0998	0.0598
1	0.0995	0.0684
1	0.1009	0.0771
1	0.1006	0.0832
1	0.1006	0.0908
1	0.1	0.0962
1	0.1	0.1016

9.神经网络权值样本

的矩阵

-0.0003	1.4996	0.1114
0.0010	-0.8895	-0.1879
-0.0008	1.0007	-0.1790
0.0006	0.6688	-0.2018
0.0005	-1.6956	0.0505
0.0004	-0.9619	-0.1823
0.0000	1.0965	-0.1699
-0.0003	1.2249	0.1555
0.0005	-0.8912	0.1879
-0.0003	0.6332	0.2036
0.0003	-0.2021	-0.2171
0.0009	-1.7340	-0.0217
-0.0001	-1.7297	-0.0267
0.0006	-1.3718	-0.1348
-0.0002	-1.4203	-0.1267
-0.0008	-0.9607	0.1823
0.0005	1.1794	0.1610
-0.0002	-1.5214	0.1066
-0.0013	-1.7410	-0.0102
-0.0007	1.5662	0.0958

的权值矩阵

-0.7230	0.9048	0.0340	-0.3546	0.0728	-0.6341	-1.0878
-0.7804	1.0115	-0.1780	0.1086	0.3968	-0.7142	-0.4737
0.9897	-1.4304	0.2776	0.2403	-1.0801	-1.3143	-0.0909
0.5139	1.1321	-1.3840	-0.8866	0.2027	0.0880	0.8417
-0.7847	0.4148	-0.9240	0.1843	-0.0587	-0.6443	-0.7613

-0.2070	-1.0837	0.1852	-0.0760	0.6968	0.0767	-0.1004
0.8627	0.0299	-0.2922	0.6816	0.7106	0.6381	0.1281
0.1788	-0.1406	-1.2258	0.2076	0.1697	0.9721	-0.4403
0.8129	0.8384	-0.9358	0.8717	0.5459	-0.1019	0.2277
-0.7660	-0.2656	-0.3723	-0.2732	-0.6195	0.1951	0.0976

-1.0444	2.5403	-1.8956	1.6311	0.5697	1.9262
-1.2993	1.8654	-0.8001	2.0897	-0.0916	1.2959
0.1931	1.1619	-0.2416	1.0940	0.6147	-0.8345
0.3543	-0.4817	0.6996	-0.4140	-0.9026	0.7450
-0.4116	-0.1089	-1.0921	-0.9064	-0.5705	1.3922

的权值矩阵

-160.5697
106.8334
-90.0593
-54.0237
165.4181
110.2566
-96.5197
-132.3848
74.4748
-77.0965
35.4486
170.2018
168.4408
141.5726
144.2084
75.7570
-121.6810
135.0404
163.1824
-153.7970