关于黄河三门峡年径流量频率线型分析
关键词：年径流量 统计分析 频率线型 三门峡 黄河
论文摘要：通过三门峡1919至1989年71a年径流量的统计分析，对P-Ⅲ、正态分布线型和对数Γ分布线型与经验频率点据拟合结果进行了比较。作为一种尝试，采用四参数对数Γ分布线型拟合三门峡年径流量资料系列进行频率特性分析，取得了较为合理的分析研究成果。研究结果表明四参数对数Γ分布线型优于P-Ⅲ和正态分布线型，验证了三门峡年径流量频率分布服从四参数对数Γ分布线型。
年径流量统计分析是水资源利用和水利电力工程规划设计的重要依据。在水文频率中,规范[1]推荐采用P-Ⅲ线型,但同时规定,经分析论证,也可采用其他线型。笔者在《广义Γ分布的特性和应用》(金光炎、董秀颖,2003) [2]研究的基础上，验证了沙坪站年最大日雨量、白蕉站年最低潮位以及沙坪水闸年最高水位观测资料系列服从四参数对数Γ分布[3] [4] [5]，本文尝试应用四参数对数Γ分布线型拟合三门峡年径流量资料系列进行频率特性的统计分析。
1.本文采用的三门峡年径流量实测资料概况
三门峡1919至1989年71a年径流量实测资料系列和推求的1470~1918年年径流量系列出自文献[6]，实测资料系列见表1。实测资料系列可通过统计学游程检验满足样本随机性要求。实测资料系列的最小值、最大值分别为241.4亿m3和802.6亿m3,极差561.2亿m3。为此将年径流量实测资料系列分为12个组限,其中组距宽度hi为61.5亿m3的10组,其他组距2组。计算在每个组限内的年径流量出现的频数fi，图1。相应的年径流量各组距区间上的经验频率为fi/n(n=71,i=1,2,…,12)。三门峡1919至1989年71a年径流量实测资料系列经验频率分组计算详见表3。在各组距区间上作以平均频率密度fi/(nhi)为高的直方图,见图3。从图1、3可看出实测资料系列直方图呈近似的正态分布形态,采用单样本K-S检验可验证其近似服从正态分布，图1中的曲线为按正态分布拟合。实测资料系列直方图有一个中间偏左主峰,两头低。中位数为491.2亿m3，在主峰区间445.95<x≤507.45亿m3上；年径流量平均值为510.93亿m3,在主峰右侧区间507.45<x≤568.95亿m3上。用矩法计算三门峡年径流量实测资料系列统计量分别为:标准差σ=114.92亿m3，变差系数Cv=0.225，偏态系数Cs=0.258，峰态系数Ce=-0.045。
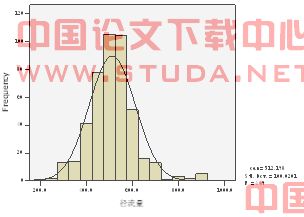
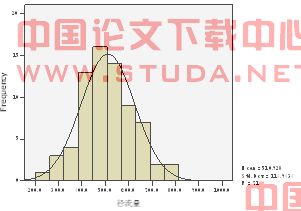
(a)实测系列 (b)推求系列
图1 三门峡年径流量资 料系列直方图
2. P-Ⅲ、正态分布和对数Γ分布线型比较分析
《水文分析与计算》(刘光文,1963)中提出了径流频率分析适线的线型选择原则[7]:⑴在计算简便的同时,具有尽量高的精度和弹性;⑵曲线与经验频率点据得到最好的拟合;⑶曲线的形状大致符合水文现象的一定物理性质,如曲线应该有一定的极限,不该出现负特征值。其中第⑵点的实质是对资料系列进行统计判别，第⑶点的实质是合理性要求。《水文频率分析述评》(金光炎,1999)也认为按照水文物理概念,曲线应该有上限,并对Slade(1936)、谢家泽(1958) 等人的研究观点作了介绍[8]。文献[9]、[10]也认为现行的频率线型在合理性方面需要完善。因此本文在上述原则的基础上对备选的3种频率线型进行比较。
2.1 P-Ⅲ和对数Γ分布线型计算方法
在采用P-Ⅲ、四参数对数Γ分布线型频率累积曲线函数拟合适线过程时，由于参数都为非线性关系形式，不能通过某种转换变为线性形式，因此只能采用非线性迭代回归的办法求解。进行非线性迭代回归时，首先确定频率累积曲线函数的表达式，确定参数的初始值，然后根据某种方法进行搜索迭代，反复调整初始值，按规范应用最小二乘法原理使得观测值与拟合值的离差平方和最小时(或者结合其他一些条件)结束迭代过程，得到各参数的最后计算结果。四参数对数Γ分布线型比P-Ⅲ线型多了1个参数，因此适线弹性要比P-Ⅲ线型大。在当今计算机技术被广泛应用于各领域的条件下,就计算方法难易程度与精度比较而言与P-Ⅲ分布线型相当。本例适线结果如图2所示，点绘在概率格纸上的经验频率点据接近直线分布形态。图中点据旁标注数字是径流量对应的年份。
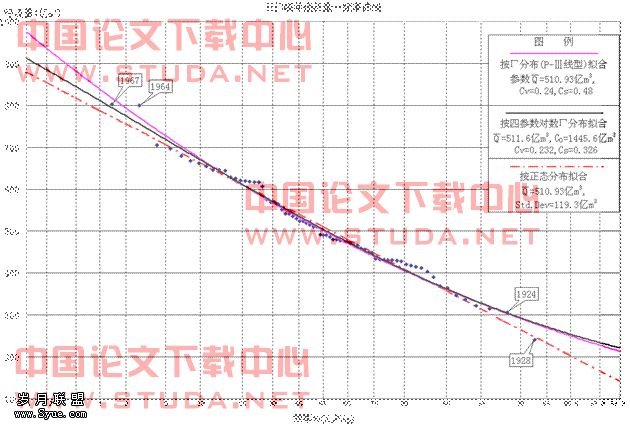
图2 三门峡年径流量-频率曲线线型比较图
2.2 P-Ⅲ、正态分布和对数Γ分布线型拟合优劣的统计判别
本例适线计算结果见表1。表1最后一行离差的SUMSQ值是观测值点据与
序 号 |
年份 径流量 | 按径流量排序 年份 径流量 | 频 率b p m (%) | P-Ⅲ线型 拟合值a 离差c | 正态线型 拟合值a 离差c | 对数Γ线型 拟合值a 离差c | |||||
1 | 1919 | 415.7 | 1967 | 802.6 | 1.389 | 817.34 | -14.74 | 773.53 | 29.07 | 794.27 | 8.33 |
2 | 1920 | 510.9 | 1964 | 799.8 | 2.778 | 770.49 | 29.31 | 739.41 | 60.39 | 755.60 | 44.20 |
3 | 1921 | 523.8 | 1937 | 706 | 4.167 | 741.46 | -35.46 | 717.59 | -11.59 | 730.82 | -24.82 |
4 | 1922 | 390.2 | 1983 | 696 | 5.556 | 719.95 | -23.95 | 701.07 | -5.07 | 712.07 | -16.07 |
5 | 1923 | 421.3 | 1949 | 679.2 | 6.944 | 702.66 | -23.46 | 687.55 | -8.35 | 696.76 | -17.56 |
6 | 1924 | 306.1 | 1958 | 667 | 8.333 | 688.07 | -21.07 | 675.98 | -8.98 | 683.68 | -16.68 |
7 | 1925 | 430.3 | 1968 | 661.2 | 9.722 | 675.38 | -14.18 | 665.78 | -4.58 | 672.18 | -10.98 |
8 | 1926 | 315.4 | 1989 | 654.3 | 11.111 | 664.09 | -9.79 | 656.60 | -2.30 | 661.85 | -7.55 |
9 | 1927 | 403.8 | 1940 | 645.9 | 12.500 | 653.88 | -7.98 | 648.21 | -2.31 | 652.44 | -6.54 |
10 | 1928 | 241.4 | 1975 | 645.6 | 13.889 | 644.53 | 1.07 | 640.45 | 5.15 | 643.76 | 1.84 |
11 | 1929 | 347.2 | 1976 | 644.6 | 15.278 | 635.87 | 8.73 | 633.21 | 11.39 | 635.68 | 8.92 |
12 | 1930 | 364.4 | 1981 | 627.9 | 16.667 | 627.79 | 0.11 | 626.38 | 1.52 | 628.09 | -0.19 |
13 | 1931 | 336.5 | 1946 | 626.2 | 18.056 | 620.20 | 6.00 | 619.92 | 6.28 | 620.93 | 5.27 |
14 | 1932 | 321.4 | 1961 | 621.3 | 19.444 | 613.02 | 8.28 | 613.76 | 7.54 | 614.12 | 7.18 |
15 | 1933 | 541.8 | 1935 | 619.4 | 20.833 | 606.20 | 13.20 | 607.86 | 11.54 | 607.62 | 11.78 |
16 | 1934 | 479.8 | 1938 | 618.3 | 22.222 | 599.69 | 18.61 | 602.19 | 16.11 | 601.39 | 16.91 |
17 | 1935 | 619.4 | 1943 | 616.9 | 23.611 | 593.45 | 23.45 | 596.72 | 20.18 | 595.40 | 21.50 |
18 | 1936 | 455.7 | 1984 | 616.3 | 25.000 | 587.45 | 28.85 | 591.42 | 24.88 | 589.62 | 26.68 |
19 | 1937 | 706 | 1955 | 607.1 | 26.389 | 581.66 | 25.44 | 586.28 | 20.82 | 584.03 | 23.07 |
20 | 1938 | 618.3 | 1954 | 575.9 | 27.778 | 576.07 | -0.17 | 581.28 | -5.38 | 578.60 | -2.70 |
21 | 1939 | 428.8 | 1963 | 568.9 | 29.167 | 570.64 | -1.74 | 576.39 | -7.49 | 573.32 | -4.42 |
22 | 1940 | 645.9 | 1985 | 568.8 | 30.556 | 565.36 | 3.44 | 571.61 | -2.81 | 568.18 | 0.62 |
23 | 1941 | 368.5 | 1966 | 564.9 | 31.944 | 560.23 | 4.67 | 566.93 | -2.03 | 563.15 | 1.75 |
24 | 1942 | 411.7 | 1959 | 551.2 | 33.333 | 555.21 | -4.01 | 562.33 | -11.13 | 558.23 | -7.03 |
25 | 1943 | 616.9 | 1933 | 541.8 | 34.722 | 550.31 | -8.51 | 557.81 | -16.01 | 553.41 | -11.61 |
26 | 1944 | 477.2 | 1945 | 541.6 | 36.111 | 545.50 | -3.90 | 553.35 | -11.75 | 548.68 | -7.08 |
27 | 1945 | 541.6 | 1951 | 535.4 | 37.500 | 540.79 | -5.39 | 548.96 | -13.56 | 544.02 | -8.62 |
28 | 1946 | 626.2 | 1982 | 529.2 | 38.889 | 536.16 | -6.96 | 544.61 | -15.41 | 539.43 | -10.23 |
29 | 1947 | 492.3 | 1978 | 524.2 | 40.278 | 531.60 | -7.40 | 540.31 | -16.11 | 534.91 | -10.71 |
30 | 1948 | 480.9 | 1921 | 523.8 | 41.667 | 527.10 | -3.30 | 536.04 | -12.24 | 530.45 | -6.65 |
31 | 1949 | 679.2 | 1988 | 519.5 | 43.056 | 522.67 | -3.17 | 531.81 | -12.31 | 526.03 | -6.53 |
32 | 1950 | 511.4 | 1979 | 514.6 | 44.444 | 518.29 | -3.69 | 527.60 | -13.00 | 521.66 | -7.06 |
33 | 1951 | 535.4 | 1950 | 511.4 | 45.833 | 513.95 | -2.55 | 523.42 | -12.02 | 517.33 | -5.93 |
34 | 1952 | 491.2 | 1920 | 510.9 | 47.222 | 509.65 | 1.25 | 519.24 | -8.34 | 513.03 | -2.13 |
35 | 1953 | 447.7 | 1947 | 492.3 | 48.611 | 505.39 | -13.09 | 515.08 | -22.78 | 508.75 | -16.45 |
36 | 1954 | 575.9 | 1952 | 491.2 | 50.000 | 501.15 | -9.95 | 510.93 | -19.73 | 504.50 | -13.30 |
37 | 1955 | 607.1 | 1970 | 490.4 | 51.389 | 496.94 | -6.54 | 506.77 | -16.37 | 500.27 | -9.87 |
38 | 1956 | 485.8 | 1956 | 485.8 | 52.778 | 492.75 | -6.95 | 502.61 | -16.81 | 496.05 | -10.25 |
39 | 1957 | 431 | 1948 | 480.9 | 54.167 | 488.58 | -7.68 | 498.44 | -17.54 | 491.84 | -10.94 |
40 | 1958 | 667 | 1934 | 479.8 | 55.556 | 484.41 | -4.61 | 494.25 | -14.45 | 487.63 | -7.83 |
41 | 1959 | 551.2 | 1944 | 477.2 | 56.944 | 480.24 | -3.04 | 490.05 | -12.85 | 483.43 | -6.23 |
42 | 1960 | 417.9 | 1973 | 476.8 | 58.333 | 476.07 | 0.73 | 485.82 | -9.02 | 479.21 | -2.41 |
43 | 1961 | 621.3 | 1962 | 475.6 | 59.722 | 471.90 | 3.70 | 481.55 | -5.95 | 474.99 | 0.61 |
44 | 1962 | 475.6 | 1971 | 471.1 | 61.111 | 467.71 | 3.39 | 477.25 | -6.15 | 470.74 | 0.36 |
45 | 1963 | 568.9 | 1977 | 466.4 | 62.500 | 463.51 | 2.89 | 472.90 | -6.50 | 466.48 | -0.08 |
46 | 1964 | 799.8 | 1986 | 465.8 | 63.889 | 459.28 | 6.52 | 468.50 | -2.70 | 462.19 | 3.61 |
47 | 1965 | 457.9 | 1965 | 457.9 | 65.278 | 455.02 | 2.88 | 464.05 | -6.15 | 457.86 | 0.04 |
48 | 1966 | 564.9 | 1936 | 455.7 | 66.667 | 450.73 | 4.97 | 459.52 | -3.82 | 453.50 | 2.20 |
49 | 1967 | 802.6 | 1969 | 447.8 | 68.056 | 446.40 | 1.40 | 454.93 | -7.13 | 449.09 | -1.29 |
50 | 1968 | 661.2 | 1953 | 447.7 | 69.444 | 442 | |||||
按年份排序
序 号 | 按年份排序 年份 径流量 | 按径流量排序 年份 径流量 | 频率b p m (%) | P-Ⅲ线型 拟合值a 离差c | 正态线型 拟合值a 离差c | 对数Γ线型 拟合值a 离差c | |||||
51 | 1969 | 447.8 | 1987 | 433.2 | 70.833 | 437.56 | -4.36 | 445.47 | -12.27 | 440.09 | -6.89 |
52 | 1970 | 490.4 | 1980 | 432.8 | 72.222 | 433.05 | -0.25 | 440.58 | -7.78 | 435.49 | -2.69 |
53 | 1971 | 471.1 | 1957 | 431 | 73.611 | 428.45 | 2.55 | 435.58 | -4.58 | 430.81 | 0.19 |
54 | 1972 | 427.6 | 1974 | 430.6 | 75.000 | 423.77 | 6.83 | 430.43 | 0.17 | 426.03 | 4.57 |
55 | 1973 | 476.8 | 1925 | 430.3 | 76.389 | 418.98 | 11.32 | 425.14 | 5.16 | 421.15 | 9.15 |
56 | 1974 | 430.6 | 1939 | 428.8 | 77.778 | 414.07 | 14.73 | 419.67 | 9.13 | 416.15 | 12.65 |
57 | 1975 | 645.6 | 1972 | 427.6 | 79.167 | 409.03 | 18.57 | 414.00 | 13.60 | 411.00 | 16.60 |
58 | 1976 | 644.6 | 1923 | 421.3 | 80.556 | 403.83 | 17.47 | 408.10 | 13.20 | 405.70 | 15.60 |
59 | 1977 | 466.4 | 1960 | 417.9 | 81.944 | 398.44 | 19.46 | 401.94 | 15.96 | 400.21 | 17.69 |
60 | 1978 | 524.2 | 1919 | 415.7 | 83.333 | 392.84 | 22.86 | 395.47 | 20.23 | 394.51 | 21.19 |
61 | 1979 | 514.6 | 1942 | 411.7 | 84.722 | 386.99 | 24.71 | 388.65 | 23.05 | 388.56 | 23.14 |
62 | 1980 | 432.8 | 1927 | 403.8 | 86.111 | 380.84 | 22.96 | 381.40 | 22.40 | 382.30 | 21.50 |
63 | 1981 | 627.9 | 1922 | 390.2 | 87.500 | 374.33 | 15.87 | 373.64 | 16.56 | 375.69 | 14.51 |
64 | 1982 | 529.2 | 1941 | 368.5 | 88.889 | 367.38 | 1.12 | 365.25 | 3.25 | 368.65 | -0.15 |
65 | 1983 | 696 | 1930 | 364.4 | 90.278 | 359.87 | 4.53 | 356.08 | 8.32 | 361.06 | 3.34 |
66 | 1984 | 616.3 | 1929 | 347.2 | 91.667 | 351.66 | -4.46 | 345.88 | 1.32 | 352.78 | -5.58 |
67 | 1985 | 568.8 | 1931 | 336.5 | 93.056 | 342.50 | -6.00 | 334.31 | 2.19 | 343.57 | -7.07 |
68 | 1986 | 465.8 | 1932 | 321.4 | 94.444 | 332.00 | -10.60 | 320.79 | 0.61 | 333.07 | -11.67 |
69 | 1987 | 433.2 | 1926 | 315.4 | 95.833 | 319.48 | -4.08 | 304.27 | 11.13 | 320.63 | -5.23 |
70 | 1988 | 519.5 | 1924 | 306.1 | 97.222 | 303.45 | 2.65 | 282.45 | 23.65 | 304.85 | 1.25 |
71 | 1989 | 654.3 | 1928 | 241.4 | 98.611 | 279.52 | -38.12 | 248.33 | -6.93 | 281.71 | -40.31 |
SUM | 36275.9 | 36206.8 | 69.09 | 36275.9 | 0.00 | 36275.9 | 0.00 | ||||
MEAN | 510.93 | 509.96 | 0.97 | 510.93 | 0.00 | 510.93 | 0.00 | ||||
MAX | 802.6 | 29.31 | 60.39 | 44.20 | |||||||
MIN | 241.4 | -38.12 | -22.78 | -40.31 | |||||||
SUMSQ | 12929.5 | 14866.3 | |||||||||
各线型拟合值的离差平方和，从而得出样数对数Γ分布总体的离差平方和为最小，故判定三门峡年径流量观测数据属于四参数对数Γ分布总体。
2.3 P-Ⅲ、正态分布和四参数对数Γ分布线型合理性分析
在P-Ⅲ线型密度函数里，随机变量的定义域为当β=2/(σ·Cs)>0时,a0≤x<+∞,其中a0= ·(1-2Cv/Cs),当Cs=2Cv时,a0=0。本例中Cv=0.24, Cs=0.48 [6],故a0=0。正态分布定义域为-∞<x<+∞。P-Ⅲ和正态分布线型都不符合《水文分析与计算》线型选择原则第⑶点的要求。四参数对数Γ分布线型当参数β<0时,随机变量的定义域为C0-A0≤x<C0，有上限和下限,符合《水文分析与计算》线型选择原则第⑶点的要求。密度函数及参数计算公式详见文献[2],[3],[4],[5],[11]。本例经过计算机程序的迭代运算求得:α=7.438312,β=-20.518372, Ao=1330.7亿m3,随机变量的上限为C0=1445.6亿m3,下限为C0- A0=114.9亿m3。因上限C0＞ 和推求系列最大值919亿m3[6],下限C0- A0＜
和推求系列最小值200亿m3[6],按正态分布计算,C0转换为标准分Z=7.84, C0- A0转换为标准分Z=-3.32,在此范围内包含了99.95%的年径流量频率分布特性,与统计学的“3σ”原则的表述“若随机变量特性值服从正态分布,那么,在±3σ范围内包含了0.9973 的随机变量特性值。因此可以断言,在±3σ范围内几乎100%地描述了随机变量特性值的总体分布。所以,在实际问题的研究中,已知研究的对象其总体服从（或近似服从）正态分布,就不必从-∞到+∞的范围去分析,只着重分析±3σ范围就可以了,因为±3σ范围几乎100%地代表了总体”相比较,同样可以认为四参数对数Γ分布的计算成果是合理的。因此在合理性方面显然优于P-Ⅲ线型和正态分布线型。
2.4 P-Ⅲ、正态分布和四参数对数Γ分布线型成果比较
从表1、图2可看出对数Γ分布和P-Ⅲ线型与丰水区的点据拟合得较好,在P=10%~99%之间两者相差较小,正态分布线型与枯水区点据拟合得较好,三种线型在P=15%~85%范围内相差不大。为了方便分析比较,现将计算成果列于表2：
表2 三门峡年径流量频率计算成果对照表
设计频率% | 0.1 | 0.5 | 1 | 80 | 90 | 95 | 97 | 99 |
P-Ⅲ线型计算成果 | 974.7 | 881.6 | 838.5 | 405.9 | 361.4 | 327.3 | 306.4 | 269.4 |
正态分布线型计算成果 | 879.7 | 818.3 | 788.6 | 410.5 | 358.0 | 314.6 | 286.5 | 233.3 |
四参数对数Γ线型计算成果 | 912.0 | 844.6 | 811.2 | 407.8 | 362.6 | 328.4 | 307.7 | 272.1 |
3. 四参数对数Γ分布线型统计假设χ2-卡方检验
若假设H0：F(x)=F0(x)为真,则年径流量x密度分布函数f(x)已知,即可求得年径流量x在给定区间里的概率P(Ai)期望值(见表3),由观测值和期望值计算χ2值。因样本个数N=71>30[11],可认为是大样本。在应用χ2-检验时计算χ2所用的期望值npi不应小于5,需将期望值npi小于5的组距合并[12],因此将样本分组数调整为m=7，四参数对数Γ分布函数参数个数l=4,则统计量ΣΔi服从自由度 df为m-l-1=2的χ2-分布。在给定的显著性水平α=0.05下,查表得置信限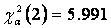
,从而有统计量χ2=ΣΔi<5.991，那么在给定的置信概率P=0.95(P=1-α)下应该接受原假设H0，即认为三门峡年径流量实测样本是来自于四参数对数Γ分布总体。
表3 χ2-卡方检验计算表
Ai | fi | pi(%) | npi | fi(1) | npi(1) | fi(1)-npi(1) |
|
x≤199.95 | 0 | 0.023739 | 0.016855 | ||||
199.95＜x≤261.45 | 1 | 0.648135 | 0.460176 | ||||
261.45＜x≤322.95 | 3 | 3.733605 | 2.650859 | ||||
322.95＜x≤384.45 | 4 | 9.952187 | 7.066053 | 8 | 10.1939 | -2.1939 | 0.4722 |
384.45＜x≤445.95 | 13 | 16.60978 | 11.79294 | 13 | 11.7929 | 1.2071 | 0.1235 |
445.95＜x≤507.45 | 16 | 19.99611 | 14.19724 | 16 | 14.1972 | 1.8028 | 0.2289 |
507.45＜x≤568.95 | 14 | 18.69182 | 13.27119 | 14 | 13.2712 | 0.7288 | 0.0400 |
568.95＜x≤630.45 | 9 | 14.1183 | 10.02399 | 9 | 10.0241 | -1.0240 | 0.1046 |
630.45＜x≤691.45 | 7 | 8.794219 | 6.243896 | 7 | 6.2439 | 0.7561 | 0.0916 |
691.45＜x≤753.45 | 2 | 4.551469 | 3.231544 | 4 | 5.2768 | -1.2768 | 0.3089 |
753.45＜x≤814.95 | 2 | 1.952254 | 1.3861 | ||||
x>814.95 | 0 | 0.928389 | 0.659157 | ||||
∑ | 71 | 100 | 71 | 71 | 71 | 1.3697 |
4.结语
⑴.规范[1]在总则1.0.7条中作了“水文计算应、实用，对 计算成果应进行多方面分析，检查论证其合理性”强制性规定。因此对水文频率分析计算作线型选择时需从数学上的适线方法、合理性检验和统计假设检验等方面进行充分的分析论证。本文应用合理性检验和统计学的χ2-检验法，从多方面来验证三门峡年径流量频率分布线型服从四参数对数Γ分布线型的统计假设。正态分布和对数Γ分布线型都可以作为三门峡年径流量频率分析备选线型用来分析比较。
⑵.笔者现已验证了三门峡年径流量、沙坪站年最大日雨量、白蕉站年最低潮位以及沙坪水闸年最高水位观测资料系列服从四参数对数Γ分布，发现了四参数对数Γ分布线型都能较好地拟合正偏、负偏、Cv较小而Cs/Cv较大以及Cs较小等类型的数据系列[3] [4] [5]。对于其他地区或其他水文资料系列，也可以开展这方面的研究，进行综合、分析和比较，并对四参数对数Γ分布线型设计值的稳健性、置信区间估计等特性作更深入的研究,以期取得更加科学合理的计算结果。
：
[1]SL 278-2002,水利水电工程水文计算规范[S].北京:水利电力出版社,2002,15-48.
[2]金光炎,董秀颖, 广义Γ分布的特性和应用[J]水文 2003,23(2):29-32.
[3]赖习知,对数Γ分布在年最大日雨量统计分析中的应用[J]广东水利水电 2006,No.6,55-57.
[4]赖习知,对数Γ分布在年最低潮位统计分析中的应用[J]水利科技与 2007,No.4,246-248.
[5]赖习知,沙坪水闸年最高水位的频率线型分析[EB/OL].防洪抗旱减灾网,http://www.rcdr.org.cn/Index/Display.asp?AdminOK=Y&NewsID=2446,2007-09-18
[6]王国安等,黄河三门峡水文站1470~1918年年径流量的推求[J]水科学进展 1999,10(2).
[7]刘光文等,水文分析与计算[M].北京:中国出版社,1963,26-29.
[8]金光炎,水文频率分析述评[J]水科学进展 1999,10(3).
[9]王国安,国内外PMP/PMF的和实践[J]水文 2004,24(5):5-9.
[10]王家祁,中国设计暴雨和暴雨特性的研究[J]水科学进展 1999,10(3).
[11]王连祥,方德植等，数学手册[M].北京:人民出版社,1979,782-878.
[12] F.S.梅里特,工程技术常用数学[M].丁仁,陈三平译,北京:科学出版社,1978,280-283.
[13]金光炎,频率分析中特大洪水处理的新思考[J]水文 2006,26(3):27-32.
[14]金光炎,水文水资源分析研究[M]南京:东南大学出版社,2003,110-127.
[15]SL 42-93,水利水电工程设计洪水计算规范[S].北京:水利电力出版社,1993.
[16]DL/T5084-1998,电力工程水文计算规程[S].北京:水利电力出版社,2002.
[17]章文波等,实用数据统计分析及SPSS12.0应用[M]北京:人民邮电出版社,2006,179-203.