当前位置：首页 > 论文 > 工学 > 水利工程

沙坪水闸年最高水位的频率线型分析

来源：岁月联盟作者：赖习知时间：2010-08-23

　　关键词：年最高水位统计分析频率线型沙坪水闸

　　论文摘要：以沙坪水闸年最高水位的统计分析为例，本文对P-Ⅲ、指数Γ分布线型和对数Γ分布线型与经验频率点据拟合结果进行了比较。作为一种尝试，采用指数Γ分布线型和对数Γ分布线型拟合沙坪水闸年最高水位资料系列进行频率特性分析，取得了较为合理的分析研究成果。研究结果表明对数Γ分布线型优于P-Ⅲ和指数Γ分布线型，验证了沙坪水闸年最高水位频率分布线型服从对数Γ分布线型。

　　洪水频率统计分析是防洪排涝决策和规划设计的重要依据。在水文频率中，规范[1]推荐采用P-Ⅲ线型，但同时规定，经分析论证,也可采用其他线型。本文在《广义Γ分布的特性和应用》(金光炎、董秀颖,2003) [2]研究的基础上，尝试应用指数Γ分布线型和对数Γ分布线型拟合沙坪水闸年最高水位资料系列进行频率特性的统计分析。

　　1.沙坪水闸年最高水位的描述性统计分析

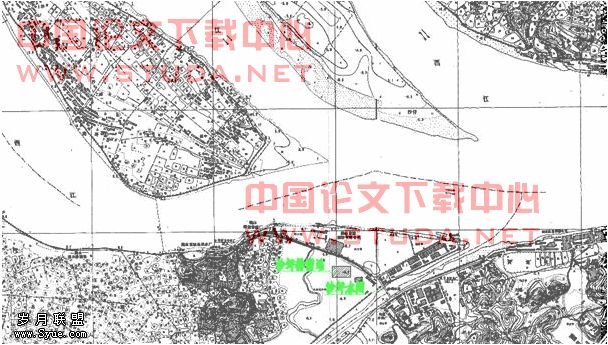
　　沙坪水闸位于西江下游右岸沙坪河入江河口处，见图1。该水闸是广东省鹤山市的一座以防洪、排涝为主，结合蓄水灌溉和改善航运的综合运用的中型水闸。该闸有从1964年自建闸以来至2006年43年的闸外年最高水位观测资料系列，见表1。资料系列的最小值、最大值分别为2.73m和6.99m,为此将年最高水位系列分为11个组限,其中组距宽度hi为0.53m的9组,其他组距2组。计算在每个组限内的年最高水位出现的频数fi，相应的年最高水位各组距区间上的经验频率为fi/n(n=43,i=1,2,…,11)。沙坪水闸年最高水位经验频率分组计算详见表3。在各组距区间上作以平均频率密度fi/(nhi)为高的直方图,见图4。从图4可看出直方图呈近似的正态分布形态,它有一个中间主峰，两头低，主峰在区间4.625＜x≤5.155m上；年最高水位平均值、中位数都落在区间4.625＜x≤5.155m上,经计算平均值为4.93m,中位数为4.78m。用矩法计算年最高水位经验系列统计量分别为:标准差σ

　　12m，变差系数Cv=0.227，偏态系数Cs=-0.0622，峰态系数Ce=-0.808。

鹤山市

图1 沙坪水闸地理位置示意图

　　2. P-Ⅲ、指数Γ分布和对数Γ分布线型比较分析

　　《水文分析与计算》(刘光文,1963)中提出了径流频率分析适线的线型选择原则[3]:⑴在计算简便的同时,具有尽量高的精度和弹性;⑵曲线与经验频率点据得到最好的拟合;⑶曲线的形状大致符合水文现象的一定物理性质,如曲线应该有一定的极限,不该出现负特征值。这一原则同样适用在年最高水位统计分析中,其中第⑶点的实质是合理性要求,《水文频率分析述评》(金光炎,1999)也认为按照水文物理概念,曲线应该有上限,并对Slade(1936)、谢家泽(1958) 等人的研究观点作了介绍[4]。因此本文在上述原则的基础上对备选的3种频率线型进行比较。

　　2.1 P-Ⅲ、指数Γ分布和对数Γ分布线型的密度函数表达式及计算方法

　　P-Ⅲ密度函数[2]为式⑴：

　　式⑴中有3个参数。密度函数的定义域为当β>0时a0≤x<∞;当β<0时,-∞< x≤a0。参数α=(2/Cs)2,β=2/(σ·Cs),a0= ·(1-2 Cv/Cs),故Cs取值不能为0。

　　四参数指数Γ分布线型[2]的密度函数如式⑵：

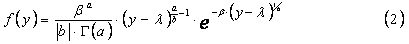
　　四参数指数Γ分布定义域为λ≤y<∞。本文以希腊字母λ代替文献[1]中的a0,以便与式⑴区别，式⑵中各参数计算公式详见文献[2],在实用范围内Cs取值可以为0或正负数值。

　　三参数对数Γ分布线型[2]的密度函数如式⑶：

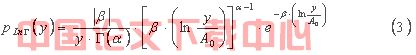
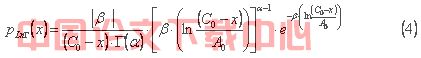
　　三参数对数Γ分布定义域为,当β>0时,A0≤y<∞；当β<0时,0<y≤A0。式⑶中使变量转换为y= C0- x, 即得四参数对数Γ分布密度函数如式⑷，函数定义域为：当参数β>0时，-∞<x≤ C0- A0；当参数β<0时，C0- A0≤x<C0。因此用四参数对数Γ分布线型进行适线时取β<0，从而使得水文随机变量具有上下极限数值。式⑷中C0是随机变量的上限, A0是随机变量的极差，α、β为分布参数。各参数与随机变量平均值、变差系数、偏态系数的关系见式⑸～式⑻。　

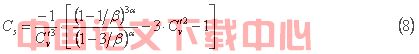
　　在采用P-Ⅲ、四参数指数Γ分布和对数Γ分布线型频率累积曲线函数拟合适线过程时，由于参数都为非线性关系形式，不能通过某种转换变为线性形式，因此只能采用非线性迭代回归的办法求解。进行非线性迭代回归时，首先确定频率累积曲线函数的表达式，确定参数的初始值，然后根据某种方法进行搜索迭代，反复调整初始值，按规范应用最小二乘法原理使得观测值与拟合值的离差平方和最小时(或者结合其他一些条件)结束迭代过程，得到各参数的最后计算结果。另外，P-Ⅲ线型可利用已有的Φ值表、四参数指数Γ分布线型可利用三参数指数Γ分布线型（克里茨基-闵凯里型）已有的模比系数Kp值表通过变量坐标的平移转换得到适线结果。四参数指数Γ分布和对数Γ分布线型都比式⑴的P-Ⅲ线型多了1个参数，因此适线弹性要比P-Ⅲ线型大。在当今计算机技术被广泛应用于各领域的条件下,就计算方法难易程度与精度比较而言与P-Ⅲ分布线型相当。本例适线结果如图2、3所示，点绘在概率格纸上的经验频率点据上部呈现出向下凹的分布

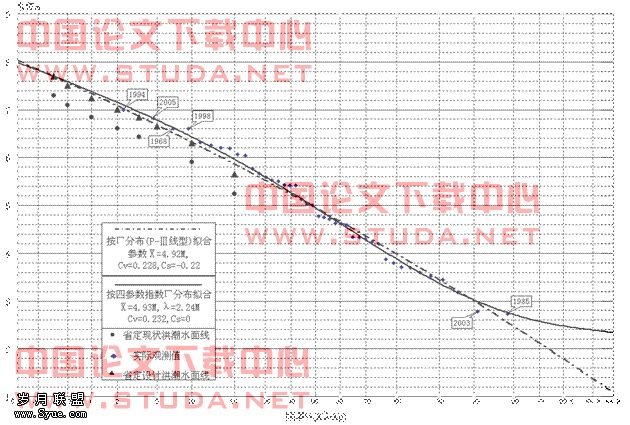
　　形态。图中点据旁标注数字是水位发生年份。

图3 沙坪水闸年最高水位-频率曲线指数Γ分布、对数Γ分布线型比较图

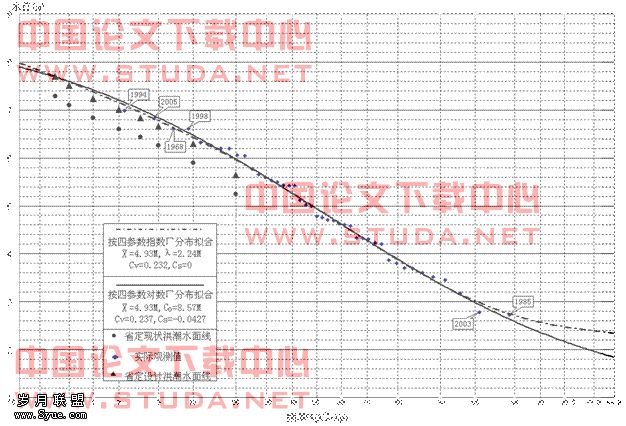
　　2.2 P-Ⅲ、指数Γ分布和对数Γ分布线型拟合优劣分析及统计判别

　　频率线型拟合优劣分析可分为：一是从适用范围上对频率线型是否与给定区域内的所有水文数据系列拟合得好进行分析，这需要对多站数据系列进行分析；二是对单站数据样本拟合优劣进行分析。本例仅就沙坪水闸年最高水位单站观测数据样本拟合优劣进行分析，因此可以应用统计学的距离分析和统计判别方法。统计判别分析是根据事物特点的变量值和它们所属的类求出判别函数，依据判别函数对未知所属类别的事物进行分类的一种分析方法。常用的判别方法有距离判别、贝叶斯判别、费歇尔判别以及逐步判别。而距离判别法较为直观，适用面广，对各类(或总体)的分布无特定要求[5]，因此本文采用距离判别法。

多个总体的距离判别是计算样本x到每个总体的距离d2(x∈Gi,i=1,2,…,k)，然后比较这些距离，如x到总体Gi的距离最短，则判x属于总体Gi。明氏距离特别是其中的欧氏距离是人们较为熟悉的,也是使用最多的距离[5]。在本例计算

序号	按时间序列排序年份水位^a		按水位大小排序年份水位^a		频率^b p_m(%)	P-Ⅲ线型拟合值^a 离差^c		指数Γ线型拟合值^a 离差^c		对数Γ线型拟合值^a 离差^c
1	1964	4.78	1994	6.99	2.273	7.03	-0.04	7.11	-0.12	7.16	-0.17
2	1965	3.52	2005	6.82	4.545	6.73	0.09	6.83	-0.01	6.88	-0.06
3	1966	6.04	1968	6.61	6.818	6.53	0.08	6.63	-0.02	6.68	-0.07
4	1967	4.61	1998	6.61	9.091	6.38	0.23	6.48	0.13	6.53	0.08
5	1968	6.61	1976	6.32	11.36	6.25	0.07	6.35	-0.03	6.39	-0.07
6	1969	4.20	1997	6.26	13.64	6.14	0.12	6.24	0.02	6.27	-0.01
7	1970	5.42	1978	6.20	15.91	6.03	0.17	6.13	0.07	6.16	0.04
8	1971	4.63	1988	6.19	18.18	5.94	0.25	6.03	0.16	6.05	0.14
9	1972	3.69	1974	6.06	20.45	5.85	0.21	5.94	0.12	5.96	0.10
10	1973	5.66	1966	6.04	22.73	5.77	0.27	5.86	0.18	5.87	0.17
11	1974	6.06	1975	5.77	25	5.69	0.08	5.77	0.00	5.78	-0.01
12	1975	5.77	1973	5.66	27.27	5.62	0.04	5.69	-0.03	5.69	-0.03
13	1976	6.32	1981	5.59	29.55	5.55	0.04	5.61	-0.02	5.61	-0.02
14	1977	5.00	1982	5.53	31.82	5.48	0.05	5.54	-0.01	5.53	0.00
15	1978	6.20	1992	5.50	34.09	5.41	0.09	5.46	0.04	5.46	0.04
16	1979	5.43	1979	5.43	36.36	5.34	0.09	5.39	0.04	5.38	0.05
17	1980	4.58	1970	5.42	38.64	5.28	0.14	5.31	0.11	5.31	0.11
18	1981	5.59	1983	5.42	40.91	5.21	0.21	5.24	0.18	5.23	0.19
19	1982	5.53	2001	5.12	43.18	5.15	-0.03	5.17	-0.05	5.16	-0.04
20	1983	5.42	1996	5.02	45.45	5.08	-0.06	5.10	-0.08	5.09	-0.07
21	1984	4.33	1977	5.00	47.73	5.02	-0.02	5.03	-0.03	5.01	-0.01
22	1985	2.73	1964	4.78	50	4.96	-0.18	4.95	-0.17	4.94	-0.16
23	1986	4.30	1993	4.75	52.27	4.89	-0.14	4.88	-0.13	4.87	-0.12
24	1987	3.45	2002	4.71	54.55	4.83	-0.12	4.81	-0.10	4.80	-0.09
25	1988	6.19	2006	4.69	56.82	4.76	-0.07	4.73	-0.04	4.72	-0.03
26	1989	3.18	1971	4.63	59.09	4.70	-0.07	4.66	-0.03	4.65	-0.02
27	1990	3.80	1967	4.61	61.36	4.63	-0.02	4.58	0.03	4.57	0.04
28	1991	3.60	1980	4.58	63.64	4.56	0.02	4.50	0.08	4.50	0.08
29	1992	5.50	1984	4.33	65.91	4.49	-0.16	4.42	-0.09	4.42	-0.09
30	1993	4.75	1995	4.33	68.18	4.42	-0.09	4.34	-0.01	4.34	-0.01
31	1994	6.99	1986	4.30	70.45	4.34	-0.04	4.26	0.04	4.26	0.04
32	1995	4.33	2004	4.23	72.73	4.27	-0.04	4.17	0.06	4.18	0.05
33	1996	5.02	1969	4.20	75	4.18	0.02	4.09	0.11	4.09	0.11
34	1997	6.26	1999	3.87	77.27	4.10	-0.23	3.99	-0.12	4.00	-0.13
35	1998	6.61	1990	3.80	79.55	4.01	-0.21	3.90	-0.10	3.91	-0.11
36	1999	3.87	2000	3.71	81.82	3.91	-0.20	3.80	-0.09	3.81	-0.10
37	2000	3.71	1972	3.69	84.09	3.80	-0.11	3.69	0.00	3.70	-0.01
38	2001	5.12	1991	3.60	86.36	3.68	-0.08	3.57	0.03	3.58	0.02
39	2002	4.71	1965	3.52	88.64	3.55	-0.03	3.45	0.07	3.46	0.06
40	2003	2.78	1987	3.45	90.91	3.39	0.06	3.32	0.13	3.31	0.14
41	2004	4.23	1989	3.18	93.18	3.20	-0.02	3.16	0.02	3.15	0.03
42	2005	6.82	2003	2.78	95.45	2.95	-0.17	2.98	-0.20	2.94	-0.16
43	2006	4.69	1985	2.73	97.73	2.55	0.18	2.76	-0.03	2.64	0.09
SUM				212.03		211.66	0.37	211.94	0.09	212.03	0.00
MEAN				4.93		4.92	0.01	4.93	0.00	4.93	0.00
MAX				6.99			0.27		0.18		0.19
MIN				2.73			-0.23		-0.20		-0.17
SUMSQ							0.7240		0.3561		0.3482

　　欧氏距离的具体过程就是求解观测值与拟合值的离差平方和。各备选线型的结果见表1。经计算P-Ⅲ适线参数 4.92m, Cv=0.228, Cs=-0.22；指数Γ分布线型适线参数取 4.93m,Cv=0.232, Cs=0, λ=2.24m；对数Γ分布线型适线参数取 4.93m, Cv=0.237, Cs=-0.0427,C0=8.57 m。表1中最后一行离差的SUMSQ值是观测值点据与各线型拟合值的离差平方和，即为样本x到各个频率分布总体Gi的欧氏距离的平方。从表1得出样本x到对数Γ分布总体的欧氏距离的平方为最小，故判定沙坪水闸年最高水位观测数据属于四参数对数Γ分布总体。

　　2.3 P-Ⅲ、指数Γ分布和对数Γ分布线型合理性分析

　　在变量的定义域方面，在P-Ⅲ线型的概率密度函数里，随机变量的定义域为当β=2/(σ·Cs)<0时,-∞<x≤a0，有上限而无下限,本例中a0=15.11m。四参数指数Γ分布线型定义域为λ≤y<∞, 随机变量有下限数值,本例中下限为λ=2.24m。P-Ⅲ和四参数指数Γ分布线型都不符合《水文分析与计算》线型选择原则第⑶点的要求。四参数对数Γ分布线型当参数β<0时, 变量的定义域为C0- A0≤x<C0, 有上限和下限，经计算机程序的迭代运算求得:α=4.459291,β=-5.777299, Ao=7.42m, 随机变量的上限为C0=8.57 m，相当于按P-Ⅲ和指数Γ线型计算的重现期分别为10068a、24931a, 随机变量的下限为C0- A0=1.15 m。因此在合理性方面显然优于P-Ⅲ线型和四参数指数Γ分布线型。为了方便分析比较,现将3种线型及广东省水利厅颁布的《西、北江下游及其三角洲网河河道设计洪潮水面线(试行)》的计算成果[6]列于表2：

表2 年最高水位频率计算成果对照表

设计频率%	0.33	0.5	1	2	3.33	5	10	20
设计洪潮水面线计算成果	7.70	7.51	7.24	7.01	6.84	6.66	6.30	5.65
现状洪潮水面线计算成果	7.29	7.10	6.84	6.60	6.43	6.26	5.90	5.24
P-Ⅲ线型计算成果	7.70	7.57	7.34	7.08	6.87	6.69	6.32	5.87
四参数指数Γ线型计算成果	7.70	7.59	7.39	7.15	6.96	6.78	6.43	5.96
四参数对数Γ线型计算成果	7.68	7.60	7.42	7.20	7.01	6.84	6.47	5.98

　　注：表中数值单位为m，计算基面为珠江基面

　　3. 四参数对数Γ分布线型统计假设χ2-卡方检验

A_i	f_i	p_i(%)	np_i	f_i₍₁₎	np_i₍₁₎	f_i₍₁₎-np_i₍₁₎
x≤2.505	0	1.575707	0.677554
2.505＜x≤3.035	2	3.965276	1.705069
3.035＜x≤3.565	3	7.737678	3.327202	5	5.7098	-0.7098	0.0882
3.565＜x≤4.095	5	11.81233	5.079303	5	5.0793	-0.0793	0.0012
4.095＜x≤4.625	7	15.07416	6.481887	7	6.4819	0.5181	0.0414
4.625＜x≤5.155	8	16.55272	7.117671	8	7.1177	0.8823	0.1094
5.155＜x≤5.685	7	15.75004	6.772516	7	6.7725	0.2275	0.0076
5.685＜x≤6.215	5	12.83426	5.518731	5	5.5187	-0.5187	0.0488
6.215＜x≤6.745	4	8.640719	3.715509	6	6.3201	-0.3201	0.0162
6.745＜x≤7.275	2	4.437336	1.908055
x>7.275	0	1.619775	0.696503
∑	43	=SUM(ABOVE) 100	=SUM(ABOVE) 43	43	43		0.3128

　　若假设H0：F(x)=F0(x)为真，年最高水位x 的　　分布函数f(x)已知,即可求得年最高水位x在给定区间里的概率P(Ai)期望值(见表3),由观测值和期望值计算χ2值。因样本个数N=43>30[7],可认为是大样本。在应用χ2-检验时计算χ2所用的期望值npi不应小于5,需将期望值npi小于5的组距合并[8],因此将样本分组数调整为m=7，四参数对数Γ分布函数参数个数l=4,则统计量ΣΔi服从自由度 df为m-l-1=2的χ2-分布。在给定的显著性水平α=0.05下,查表得置信限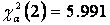,从而有统计量χ2=ΣΔi<5.991，那么在给定的置信概率P=0.95(P=1-α)下应该接受原假设H0，即认为沙坪水闸年最高水位样本是来自于四参数对数Γ分布总体。

　　4.结语

　　⑴规范[1]在总则1.0.7条中作了“水文计算应、实用,对计算成果应进行多方面分析，检查论证其合理性”强制性规定。因此对水文频率分析计算作线型选择时需从数学上的适线方法、合理性检验和统计假设检验等方面进行充分的分析论证。本文应用合理性检验和统计学的χ2-检验法,从多方面来验证沙坪水闸年最高水位频率分布线型服从四参数对数Γ分布线型的统计假设。四参数指数

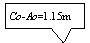
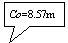图4 年最高水位频率密度分布直方图

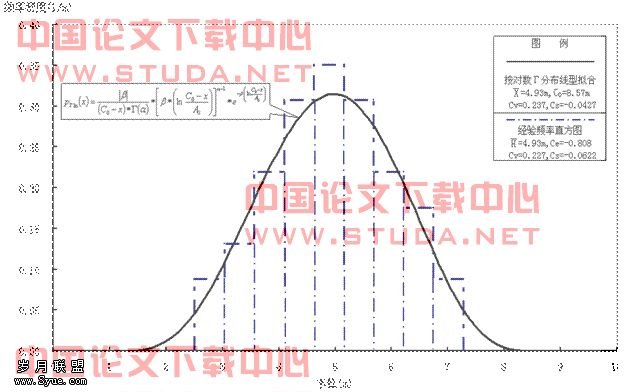
　　Γ分布和对数Γ分布线型都可以作为沙坪水闸年最高水位频率分析备选线型用来分析比较。⑵关于洪水的上限值大小问题,我国王国安的研究(1999)认为,从物理成因上看,大流域PMF的洪峰流量,一般都应小于皮尔逊Ⅲ型曲线的万年一遇值[9]。从合理性分析年最高水位上限值C0应大于PMF的洪峰流量对应的水位值。因此本例采用四参数对数Γ分布线型适线得出的水位上限C0=8.57 m,相当于按P-Ⅲ线型和指数Γ线型计算的重现期分别为10068a、24931a,可认为上限C0是合理的。⑶本例的计算成果与广东省水利厅颁布的《西、北江下游及其三角洲网河河道设计洪潮水面线(试行)》的计算成果[6]比较，是偏于安全的(见表2)。对于其他地区或三角洲河网更大区域范围内,也可以开展这方面的研究,进行地区范围内的综合、分析和比较,并对四参数对数Γ分布线型设计值的稳健性、置信区间估计等特性作更深入的研究,以期取得更加科学合理的计算结果。⑷参照[10]的研究观点，沙坪水闸年最高水位系列也可通过正态分布统计假设检验近似服从正态分布,见图4。因上限C₀＞ ,下限C₀- A₀＜ ,下限C0- A0＜ ,按正态分布计算在此范围内包含了99.91%的水位频率分布特性，与统计学的“3σ”原则[14] 的表述“若随机变量特性值服从正态分布，那么，在±3σ范围内包含了0.9973 的随机变量特性值。因此可以断言，在±3σ范围内几乎100％地描述了随机变量特性值的总体分布。所以，在实际问题的研究中，已知研究的对象其总体服从（或近似服从）正态分布，就不必从-∞到+∞的范围去分析，只着重分析±3σ范围就可以了，因为±3σ范围几乎100％地代表了总体”相比较，同样可以认为本文的研究成果是合理的。