摘  要  本文对数学形态学中的腐蚀和膨胀的原理和中值滤波除噪应用进行研究，针对二值化图像把中值滤波与腐蚀相结合研究一种边缘检测的方法，通过Visual C++6.0仿真实现，得到满意的效果。该方法能够有效地去噪，检测图像中的细节，定位准确，并且量小，效率高。    关键词  数学形态学; 中值滤波; 腐蚀; 边缘检测 0  引言     图像边缘是图像最基本的特征, 边缘中包含着有价值的目标边界信息，这些信息可以用于图像分析、目标识别以及图像滤波。边缘检测是图像处理的重要内容，是模式识别和计算机视觉的基础^[1]。所谓边缘(或边沿)是指其周围像素灰度有阶跃变化或屋顶变化的那些象素的集合^[2] ,边缘检测是图像工程的一个重要内容。数学形态学的主要用途是获取物体拓扑和结果信息，它通过物体和结构元素相互作用的某些运算，得到物体的本质形态。随着数学形态学理论的不断完善与.数学形态学在图像边缘检测中得到了广泛的研究和应用。边缘检测的难题是检测精度与抗噪性能之间的矛盾.图像普遍存在噪声。图像边缘和噪声均为频域中的高频分量，这给边缘检测带来了困难。针对以上问题,本文重点研究数学形态学的基本原理并结合图像中值滤波分析数学形态学在边缘检测中的应用。

1  数学形态学的基本原理

    数学形态学是分析几何形状和结构的数学方法,是建立在集合代数基础上,用集合论方法定量描述几何结构的。数学形态学是一组形态学的代数运算子组成。用这些算子及其组合进行图象形状和结构的分析处理包括图象分割、特征抽取、边缘检测等方面的工作^[3]。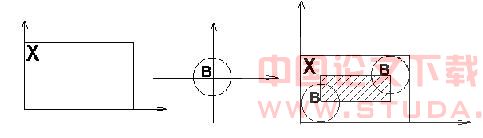

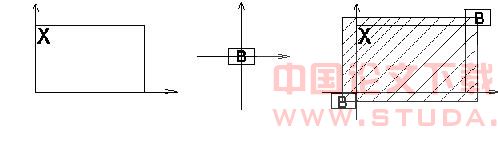图1.1  腐蚀的基本原理    腐蚀是把结构元素B平移a后得到Ba，若Ba包含于X，我们记下这个a点，所有满足上述条件的a点组成的集合称做X被B腐蚀的结果。用公式表示为：E(X)={a| Ba∈X}=XθB如图1.1所示。膨胀可以认为是腐蚀的对偶运算，其定义是：把结构元素B平移a后得到Ba，若Ba击中X，我们记下这个a点，所有满足上述条件的a点组成的集合称做X被B膨胀的结果。用公式表示为：D(X)={x|B[x]∩x≠ф} =X⊕B 如图1.2所示：图1.2  膨胀的基本原理    在数学形态学中，最为重要的两个组合运算是形态学开运算和闭运算。我们可以利用腐蚀和膨胀来定义开运算和闭运算。先腐蚀后膨胀称为开运算，即OPEN(X)=D(E(X)) 。开运算可以消除散点和毛刺即对图像进行平滑。先膨胀后腐蚀称为闭运算，即CLOSE(X)=E(D(X)) 通过选择适当的元素结构可以通过闭运算将两个邻近的目标连接起来。开运算使图像变小，闭运算使图像增大。开闭运算有一个有趣的性质等幂性，它意味着一次滤波就能把所有特定于结构元素的噪声滤除干净，重复运算不会再有效果。这与经典方法（如中值滤波，线性卷积）不同。[4]研究了膨胀和中值滤波结合在边缘检测中的应用。本文介绍腐蚀和中值滤波结合在边缘检测中的应用。

2  基于中值滤波和数学形态学的图像边缘检测方法

    分别采用邻域平均和中值滤波对有噪声的二值图片进行处理，处理结果如图2.1所示。通过对图2.1的分析可知，采用中值滤波的效果要比采用邻域平均处理的滤波效果好,主要是中值滤波后图像的轮廓比较清晰,故本文采用中值滤波处理原图像。     原图                         邻域平均                    中值滤波图2.1   采用不同滤波后图像效果    中值滤波是基于排序的非线性滤波的典型，他被成功地应用于保留需要的图像结构的同时消除（脉冲）噪声。中值滤波可用如下步骤完成：   （1） 将模板在图像中漫游，并将模板中心与图中某个像素位置重合   （2）读取模板下各对应像素的灰度值   （3）将这些灰度值从小到大排成一列   （4）找出这些值中排在中间的一个    （5）将这个中间值赋给对应模板中心位置的像素^[5]。    文中使用3Χ3的中值滤波模板。经过中值滤波后，图像噪声被去除，而且图像边缘保护得比较好，再运用基于腐蚀运算的边缘提取算法对图像进行腐蚀运算，使图像边缘上的灰度得到加强，再用原图像减去腐蚀后的图像，从而得到图像的边缘。本文利用采用3x3模板元素对图像进行腐蚀。设原图像为F, 滤波后输入的图像为A, B是“结构元素”则A被B腐蚀可以表示为:M=AθB,利用原图减去腐蚀后的图像，则可获得图像的边缘:H=A-M=A- Aθ B。其原理如图2.2所示，理论分析可知，与[4]提到方法相比，通过本文方法能够更准确地检测到图像的边缘。A              B                M                           H图2.2  腐蚀检测边缘的原理图

3  试验结果分析

     使用Visual C++6.0对文中所用方法编程实现并且与其他的边缘检测算法结果比较，如图3.1~图3.4所示。图3.1canny算子        图3.2 susan算子     图3.3 文献[4]方法     图3.4 本文方法    由上图我们可以看出，canny算子和susan算子两种算法提取的边缘细节损失都比较多，且边缘连续性差，容易将噪声点当作边缘点来检测，边缘轮廓不清楚，精确度小。本文所采用的基于中值滤波和数学形态学结合的算法所提取图像边缘细节损失少，图像质量比较好，所提取边缘细节、边缘连续性好,可以应用于细小边缘的检测，例如细小缺陷的边缘检测。通过图3.3和图3.4的比较可以知道，与文献[4]所用方法相比，采用本文方法进行边缘检测能够保留更多的细节。

4  结论

    本文针对二值化图像（可推广到灰度图像）采用中值滤波和数学形态学中的腐蚀相结合的方法，理论分析和仿真试验都证明方法的有效性.该方法能够很好地去噪,检测图像中的细节，定位准确，连续性较好，并且易于软件编程并行实现，量小。

文献

[1] 李刚，黎燕.数学形态学的二值图像的边缘检测.可靠性与环境适应性理论研究，2004年12月[2] 何东健.数字图像处理. 西安：西安科技大学出版社，2003年， 90-91[3] 何斌等.VsualC++数字图像处理.北京：人民邮电出版社 ，2001年4月，335-336[4] 周俊霞，吴国平，高芳芳.于中值滤波和数学形态学结合的边缘检测.计算机总第205期，2004年 8月[5] 章毓晋.像工程（上册）.第二版.北京：清华大学出版社，2006年3月，102-103