摘  要  曲面造型一直是机图形学的重要研究内容之一。曲面的显示效果涉及到数据的存储结构及对数据的操作方法等多方面的知识。网格细分是曲面的一种表示方法，但却是目前广泛使用的一种曲面造型方法。而三角网格细分的许多算法已经成功地应用于许多领域。本文介绍了曲面造型的相关理论，重点介绍了Loop细分算法及其在重建隧道三维结构中应用。     关键词  曲面; 网格; 细分; 逼近; 隧道 

0  引言

    隧道的施工安全，常常与隧道的掌子面观察紧密联系。现行观察一般是人工纪录和掌子面状况描绘或者照像，这种描绘往往由于人为因素，使获得的数据缺乏一致性和可比性。而照片在冲洗过程中，由于相片本身的分辨率也会导致冲照片在洗过程中出现信息畸变、丢失的现象，而且不能数字化和及时处理。因此在对隧道开挖过程中的掌子面图象进行处理后，就需要根据所获得的特征参数，重建、显示隧道的三维结构，并用以指导隧道的施工。但三维结构在重建过程中，重建的效率是十分重要的。本文利用曲面网格的相关理论，并结合三角网格细分算法来进行遂道三维结构的重建，以加快生成速度和提高隧道三维结构显示的质量。

1  曲面网格的构建

    空间曲面的构建一般采用参数方式。若用双参数构建曲面，其数学形式为：S=S(u,v)=[x(u,v),y(u,v),z(u,v)]  (a≤u≤b,c≤v≤d)      当u,v在各自的定义域内变化时，S（u,v）在空间坐标系中变化，且O-UV坐标系中的任意一点(u,v)均与O-XYZ坐标系中的点(X,Y,Z)呈一一映射关系。当v不变而u变化时，得到u线；反之，则得到v线。所有的u线和v线所形成的网叫参数曲线网。由曲线p(u,c),p(u,d),p(a,v),p(b,v)四条边界曲所围成的部分，被称为网格，它定义在矩形域（(a≤u≤b,c≤v≤d)）上。矩形定义域一般采用正方形（0≤u≤1,0≤v≤1）。Coons曲面，Bezier曲面，B样条曲面均可用这种方式来建构。    曲面建构方法亦可用三角域方式来构建。选取三角形区域{（u,v,w）|u≥0,v≥0,w≥0,u+v+w=1},并采用B—网来构建曲面。对于不共线的三点P₀,P₁,P₂可以构成一个三角形，该三角形所在的面上任一点P可表示为P（u,v,w）=uP₀+vP₁+wP₂  (u+v+w=1)    若当0≤u+v+w≤1,则点P(u,v,w)位于P0，P1，P2所构成的三角形之内。例如三角域上的n次Bezier曲面（三角域上的三次Bezier曲面如图1）为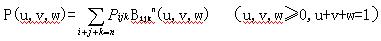   （1）    B_ijkⁿ(u,v,w)是与点 P_ijk对应的基函数，且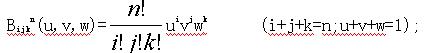

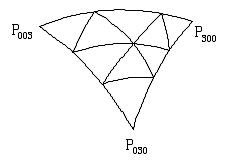
  图1  三角域上三次Bezier曲面    B样条曲面亦可采用三角域来构建，但基函数形式与建构Bezier曲面的基函数不同。

2  网格的细分（Subdivision）

2.1  曲面造型一直是计算机图形学的重要研究内容之一。网格细分(Subdivision) 是曲面的一种表示方法,是曲面造型的一个分支。该方法实际上是从一个被称为控制网格(绝大多数网格数据可用数字化仪通过人工模型来输入) 的多面体开始,递归地计算新网格上的每个顶点(这些顶点一般是其上一级细分网格上某几个顶点的加权平均),从而产生新的小面来获得更好的图形显示。这种方法只要计算机的硬件条件允许，就可以不断进行下去。    针对网格构建方法，产生了网格细分的许多算法（网格细分算法的思想可以追溯到50 多年前G. de Rham用于生成二维光滑曲线的“砍角算法”）。常见的有Catmull-Clark 算法、Loop算法、蝶形算法、Doo-Sabin 算法， 算法等。一般而言，网格的细分造型可分为两步:拓扑分裂和几何平均。拓扑分裂定义了细分增加的网格点的拓扑结构,几何平均确定网格点的几何位置。2.2  三角网格细分法的特点:任意拓扑、可伸缩性、表示的一致性、数值稳定性、简单性。正是由于三角网格具有上述特点,使得三角网格细分方法作为一种CAGD技术具有很强的生命力。

3  经典的网格细分算法---Loop算法

 3.1  Loop 细分算法是美国犹他大学的Charles Loop 于1987 年在其硕士中提出的一种逼近型三角形面分裂细分算法。它是基于B样条逼近型算法的一种策略,应用于规则网格时可以产生C²连续的曲面,在非正规点处则可达到C¹ 连续。该算法使每个三角片在分裂后生成四个小的三角面片，如图2。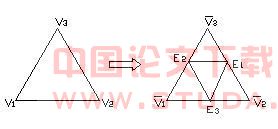

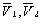图2  一个三角面片上的Loop细分格式    根据点生成方式的不同可将新生成的点分为现两类:    (1)第一类控制点：由原三角形的边生成的对应控制点，如E₁，E₂等；    (2)第二类控制点：由原三角形的顶点生成的对应控制点，如等。3.2  对于规则的三角网格，Loop细分格式如图3所示：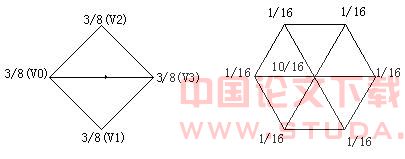

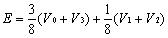(1)第一类点                            （2）第二类点图3  规则网格上Loop细分格式下各顶点的权    由原三角形的边生成的第一类控制点由下式进行： (2)    由原三角形的顶点生成的第二类控制点由下式进行计算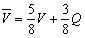：                  (3)    其中，V ₀、V ₁、V ₂、V ₃ 是与第一类点相邻的两个三角形的顶点,V 是原始控制顶点,Q 是与V有一条边相连的原始控制顶点的和的平均。3.3 对任意三角网格,运用相同的规则生成第一类控制点和第二类控制点, 但第二类控制点的权修改为如图4所示。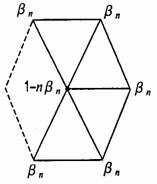

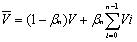图4　非规则网格上第二类控制点的权    此时公式（3）应为：       

 （4）

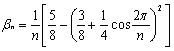    其中 。当n=3时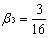， ,当n>3时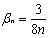， ；V_i( i=0,1,2,…,n-1) 是与V 有一条边相连的原始控制顶点。

4 

    三角网格细分方案是目前广泛应用的曲面建构方法,在隧道掌子面三维重建过程中如果能有效地利用三角网格细分方法,不但可以有效地减少数据的存储量,而且可以改善建模的生成速度和模型的显示效果。更重要的是不仅能够根据获得的特征参数，重建、显示隧道的三维结构，而且能够根据重建的隧道的三维结构，进行一定范围内的地质情况的预测，从而更加安全、高效地指导隧道的施工。

[1]  Loop C. Smooth Subdivision Surfaces Based on Triangles. Master’s thesis,Department of Mathematics,University of Utah,1987[2]  Loop C. Triangle Mesh Subdivision with Bounded Curvature and the Convex Hull Property. Microsoft Corporation,2001[3]  张学辉.三角网格细分技术在三维地质模型中的应用.技术与工程[J]. 2006年1月第1期,84-85[4]  王金生等.几种经典网格细分算法的比较. 计算机应用研究[J]. 第六期, 139-141[5]  韩越兴等.Loop细分模型的边界拼接算法.大连理工大学学报[J]. 第44卷第1期, 2004年1月,  12-16[6]  刘加猛等.Loop细分格式在基于Java 3D 的几何造型系统中的应用.计算机应用[J],  第24卷第6期 2004年6月,  129-130