用Excel探究自由落体运动实现过程
“探究自由落体运动”是通过打点计时器记录下重物自由下落的运动轨迹,根据其仅受重力作用,故猜想自由落体运动是最简单的变速运动即匀变速直线运动。作为一个让中学生自己探究的活动,如何才能做到既科学严谨又操作简单快捷地验证该猜想呢?笔者尝试采用Excel来帮助学生完成这个任务,下面是具体的实现过程。
设计验证思路
我们利用打点计时器记录自由落体运动轨迹时,得到的轨迹如图1所示。如何通过纸带的信息验证自由落体运动是匀变速直线运动呢?实验验证的方法很简单:通过测量出纸带上各点的位移,只要证明纸带上各点的位移与对应时间的平方成正比,或证明各时刻的速度均匀增加,便可证明自由落体运动是匀变速直线运动。
![]()
图1
输入实验数据
在Excel软件工作簿的某一列(本文为了方便介绍称此列为第一列)的单元格中依次输入各点测量时间。在其相邻的一列(称第二列)中输入对应的位移值,实验测量的数据是以毫米为单位的,为了使输入快捷些,我们在该列直接输入以毫米为单位的位移值。在第三列的第一行输入“=”号,然后点击第二列第一个数据,再输入 “?10^-3”,即得到“=B2?10^-3”,按“回车键”,再点击该数值出现一“十”字光标,拖动光标往下拉,得到一组数据,该组数据实际上是把第二列的数据转化成以米为单位的位移值(如图2)。
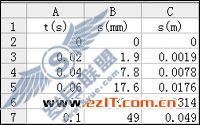
图2
建立s-t图像
选中第一列和第三列数据,选中下拉菜单“插入”中的“图表”,便弹出“图表向导”对话框,在“标准类型”项中选择“X-Y散点图”,接着按照“图标向导”的提示,便可一步步得到所要画的s-t图像。其中要设置的是“图标向导-4步骤之3-图表选项”,在该项中我们可以输入图表标题,X轴、Y轴标题,还可以对坐标轴、网格线、图表位置等进行设置。
添加趋势线并显示曲线表达式
移 动鼠标至生成的s-t图表中某一散点,点击鼠标右键,选择“添加趋势线”命令,便出现“添加趋势线”对话框,其中的“类型”标签中有“线性”、“对数”、“多项式”等几种可选择的回归分析类型,选中“多项式”。在另一个标签“选项”中选中其中的“显示公式”项,再点击〔确定〕,即可将各点趋势线描出并将该曲线的表达式显示出来(如图3)。由于测量数据的误差,拟合出来的“位移-时间”表达式为y=4.9152x2-0.0011x-2E-05,但是我们可以看到其中的x项系数及常数项相对x2项系数小得多,故这两项可视为误差,忽略不计,即得y=4.9152x2。这样我们便简单快捷地证明了纸带上各点的位移与对应的时间平方成正比。

图3
现在我们来证明各时刻的速度是均匀增加的,根据自由落体运动物体在某一时刻速度为vt=2s/t(s和t分别为该点的位移和时间,该证明课本已有详述)。根据该式我们可以得出物体在各个时刻的速度,只需在上面的位移数据后一列第三行输入“=C3?2/A3”,然后按“回车键”,再点击该数值出现一“十”字光标,拖动光标往下拉,得到物体在各个时刻所对应的速度数据。选中时间数据和速度数据,再通过图表向导、设置图表、添加趋势线、显示曲线公式等步骤,便可生成如图4的v-t图表。其过程与上面类似,惟一不同的是在“添加趋势线”对话框的“类型”标签中应选择“线性”而不是“多项式”。我们得到“速度-时间”关系表达式为y=9.831x-0.0029,很明显常数项比x项系数小得多,可视为误差不计,故可得到各点速度正比于时间,物体作匀变速直线运动且其加速度为9.831。

图4
实践证明:以上这种通过让学生学会利用计算机来处理实验数据,自主探究物理规律的活动,对加深学生理解课本知识,提高学生的科学创造力和培养学生处理信息能力都是很有益的。