关于新课程理念下“问题情境”的有效教学问题与思考

　　摘要:问题情境的创设是课堂教学的一个环节.在新课程理念下，只有创设有效的问题情境，才能真正发挥问题情境的搭桥与引路功能本文探讨了有效的问题情境的六个特征，提出了有效的问题情境的六种教学方式，旨在通过创设适宜的、有效的问题情境，让学生产生强烈的情感共鸣，激发学生的求知欲望，同时充分暴露数学思想的发生和过程，吸引学生积极参与知识的再发现和自主构建.
　　论文关键词:问题情境;有效;教学;思考
　　古语云:“学起源思，思起源疑.”数学问题情境是学生掌握知识，形成能力，培养理性思维，发展良好心理品质的重要源泉，是沟通现实生活与学习的桥梁.创设良好的“问题情境”，能激发学生的学习兴趣和动机，使学生产生“疑而未解，又欲解之”的强烈愿望，进而转化为一种对知识的渴求，为课堂教学创设一种紧张、活跃、和谐、生动、张弛有道的理想氛围.而在实际教学中，有些教师对问题情境设计关注不够、认识模糊，认为只有生活实例才是情境，似乎每节课都要实际情境，因而频频出现低效、无效、多余，乃至干扰学习的“假情境”.那么在新课程理念下如何进行有效的“问题情境”的创设，使数学课堂充满生命活力呢?
　　一、新裸程关于“间题情境”有哪些理念
　　《全日制义务数学课程标准(实验)》提出:“让学生在生动具体的情境中学习数学.”“要让学生在现实情境中体验和理解数学.”“数学教学是数学活动的教学，是师生之间互动与共同发展的过程.数学教学要紧紧联系学生的生活实际，创设各种情境，为学生提供从事数学活动的机会，激发对数学的兴趣，以及学好数学活动的愿望.”
　　《普通高中数学课程标准(实验)》指出:“数学教学要紧密联系学生的生活实际，从学生的生活经验和已有的知识出发，创设生动有趣的情境，从而提高学生的学习效率.”“教师要创设恰当的问题情境，鼓励学生发现数学和问题解决的途径，使他们经历知识形成的过程.”
　　以上说明，新课程强调让学生在现实情境和已有的生活、知识经验的基础上学习和理解数学，“问题情境一建立模型斗解释与应用”是数学课程标准倡导的教学模式，促使教学真正成为教师和学生富有个性化的创造过程.良好的情境可以使教学内容触及学生的情绪和意志领域，使学生把学习活动变成自己精神的需要，因此课堂教学中非常重要的一点就是为学生创设适宜的问题情境，激发学生学习兴趣，真正调动起学生思维的积极性，使得课堂教学既充满活力又富有成效.
　　二、怎样的问题情境是合适的、有效的
　　案例1在苏教版《必修1》“2.5.2用二分法求方程的近似解”的教学中，两位教师分别设计了如下问题情境.
　　问题情境1:某人现有1万元现金，他有两种选择:存进银行或购买国债，已知银行的年利率为2.25%(计复利)，购买国债的年利率为2.98%(计单利).问:
　　(1)若存10年，是存进银行好还是购买国债好?
　　(2)若存20年，是存进银行好还是购买国债好?
　　(3)若存30年，是存进银行好还是购买国债好?
　　(4)存几年，购买国债的本利和与存银行的本利和一样多?
　　问题情境2:猜一个在10-99之间的数，猜10次能不能猜出来?有人说，猜7次一定能猜出来，你认同他的观点吗?为什么?
　　问题情境1通过与学生密切相关的生活问题让学生认识到有些方程的解无法精确求出，从而激发学生去寻求近似解，在寻求近似解的过程中，感悟二分法.在实际教学中，学生对计单利与复利不熟悉，且本问题运算较为困难，耗时过多，教学效果不容乐观.再次审视该情境，发现效益低的症结在于—选择问题过长且运算过繁，这使得课堂上时间分配极不合理，直接影响学生在本课教学中领悟二分法本质的结果。
　　问题情境2以猜数字这一常见的娱乐方式开始，一下子将学生吸引住，在猜数字的过程中，学生逐步感悟到取中间数的好处，为后续研究方程的近似解埋下伏笔。
　　什么样的问题情境才算有效呢?有效问题情境就是呈现给学生刺激性教学信息，是学生掌握知识，培养能力，开阔思维，发展心理品质的重要源泉.创设的有效问题情境能激发学生的好奇心和求知欲，产生认知冲突，使学生主动地学习.有效问题情境，除了依照问题设计规律及教育目的、数学学科特点，具有数学因素与必要的形式外，至少必须满足以下几个特征:
　　第一，趣味性.问题情境的设计要充分挖掘教材的趣味因素，使课堂产生愉快的学习氛围，能吸引住学生，调动学生的学习积极性.
　　第二，量力性.所创设的问题情境的难度应该趋向于学生思维的“最近发现区”，使学生可以“跳一跳，摘桃子”.问题情境的创设要符合学生一般认知规律、身心发展规律，包括学生的知识经验、能力水平、学习习惯、生活经历及基本心理状况等.
　　第三，直观性.能够提供某种直观，符合数学学科特点，使学生借助于这种直观，领悟数学实质，提炼数学思想方法，灵活运用数学.
　　第四，开放性.问题富有层次感，人手较易.开放性强，解决方案多，学生思维与创造的空间较大.
　　第五，探究性.问题情境能引起学生的认知冲突和探究的欲望，能激发兴趣，启迪学生的思维，促进学生主动地参与探究。
　　第六，体验性.能给学生提供深刻体验，人人有所得，学生能够感受、体验数学.并有助于学生发现问题，提出问题。
　　三、创设有效的问题情境的主要教学方式
　　有效的问题情境其教学功能主要表现在激发学生的认识和情感，营造学生渴望生成新知识的认知环境，启发学生的思维，让学生迅速投人到课堂教学状态中去。
　　按照数学知识的发生发展过程以及学生的认知规律，以教材内容为载体，通过精心设计问题情况，引起学生认知冲突，点燃学生思维的火花，激发学生探究的欲望.有效的问题情境应符合以下要求:①符合学生的经验(生活的、数学学习的)，能激发学生学习的热情和好奇心;②能反映数学的本质;③能引发学生思考，并能迅速引人主题.
　　1.创设趣味性问题情境
　　设计问题情境时要新颖别致，使学生学习数学感到有趣味感、新鲜感.能激起学生思考、讨论的兴趣.如利用刁尼秀斯之耳的故事为背景介绍椭圆的光学性质，学生抱着极其浓厚的兴趣去学习，求知欲一旦被调动就不愁教学的效率了.在新课中，教师注意引用部分贴近学生生活的事例.如讲授“充要条件”时，为了让学生感受“生活中数学的思维”，增加对学习逻辑知识的兴趣和信心，设计了如下具有浓郁的文化气息的问题:请试探讨下列生活中名言名句的充要关系:①水滴石穿;②)骄兵必败;③名师出高徒.
　　2.创设现实性问题情境
　　案例2关于“基本不等式”，苏教版《必修5》中的问题情境为:一个天平的两臂长略有不同(其他因素不计)，把一个物体放在天平左边，称得其质量为a，放在天平的右边，称得其质量为b，若取“平均” 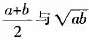你认为正确吗?取(算术)平均值是人们“习惯性”的做法，生活实际中人们可能常会犯这样的错误，但从物理的角度仔细想一想，学生不能算出物体的质量为，这时自然提出一个问题: 具有怎样的大小关系？用这样的现实性问题情境引人非常自然，它就像高速公路的“引桥”，短而有效地引导人们顺利地进入高速公路.
　　3.创设实验性问题情境
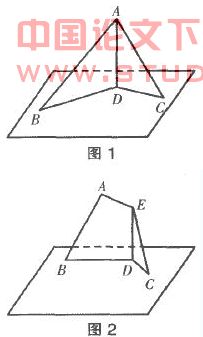
　　案例3在直线与平面垂直的判定的教学中可以设计如下实验:要求学生将准备好的只角形纸片任意折叠，只要保证翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)使得折痕与桌面垂直即可.学生动手实验后主要翻折出以下两种情形:
　　就此提出问题：
　　(1)这两条折痕D，DE是怎样得到的?(是通过翻折使日D，Dc重合得到的)
　　(2)按图l、图2翻折后，都能使得折痕与桌面所在的平面垂直。那么两者间必定存在共同的特征，你认为两者共同的特征是什么?然后引导学生通过类比，归纳出两科情形的共同本质特征，进一步让学生概括出直线与平面垂直的判定定理.
　　通过数学实验，改变了传统教学模式下数学过分强调形式化的逻辑推导和结果，经过学生的动手操作、观察比较、类比归纳，给学生创造了大胆猜想和发现的机会，自主发现数学知识，亲历知识形成的过程，使学生在实践中感受到数学探索的乐趣，获得成功的体验.
　　4.创设开放性问题情境
　　案例4直线y=2x+m与抛物线Y=xz相交于A,B两点，——，求直线AB的方程.(需要补充恰当的条件，使直线方程得以确定)
　　此题一出现，学生的思维便很活跃，补充的条件形形色色.
　　例如:a IABI=2;
　　B 
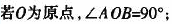
　　c AB中点的纵坐标为6
　　d AB过抛物线的焦点F.
　　涉及的知识有韦达定理、弦长公式、中点坐标公式、抛物线的焦点坐标，两直线相互垂直的充要条件等，学生实实在在地进人了学习状态。
　　上面创设的开放性问题情境，有较大的思维空间，让不同层次的学生都能在这个问题情境中有不同的层次的施展.
　　5.创设阶梯式问题情境
　　设计问题应合理配置几个级别的问题，对知识的重点和难点，应像攀登阶梯一样，由浅人深，由简到烦，达到掌握知识，激活思维的效果。
　　案例5如教学“直线与圆锥曲线的位置关系”时.设计如下问题链:已知椭圆C:①请你具体给出一组a,b的值，使直线l与椭圆相交;②直线l与椭圆C相交时，a,b应满足什么关系;③若a+b=1，试判定直线L与椭圆C的位置关系。
　　问题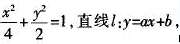①给学生提供了自由想象空间，使不同层次的学生不仅可以从“形”的角度直觉探索“直线与椭圆的位置关系”，去寻找一组符合题意的a,b值，而且还能从“数”的角度引发思考，转化为“解二元一次方程组”的问题，从而在解决②小题时，水到渠成，使学生的思维始终处于一种积极主动的状况，从而培养发现问题、提出问题的意识.
　　6.创设示错式问题情境
　　思维的动力来源于学生认知结构的不协调，而示错就是故意制造或扩大这种不协调.学生的思源于疑，疑源于错，示错得体，犹如一石投人学生脑海，必将激起学生思维的浪花，荡起智慧的涟漪，从而激起学生强烈的探求新知的欲望和动力.通过示错一纠错~醒悟的教学过程，让学生在错误中寻找疑点，在误中思，在思中悟。
　　案例6在讲基本不等式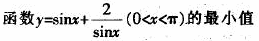的应用时，可提出这样的问题让学生判断.由于学生常常受公式的束缚‘往往根据就断言这个函数的最小值为此时教师可进一步提出问题:如果这个函数的最小值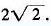是，那就意味着不等式中等号能成立，请问这个不等式中的等号何时成立?
　　此时学生就会发现只有当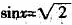时等号才成立，而这是不可能的.
　　这样，学生今后在应用公式 求最值时，不但会注意到x,y为正数及和(或积)为定值，还会注意到等号能不能成立，
　　总之，一个有效的问题情境就如同桥梁，联系旧知与新知边a同序幕，预示着高潮与结局;如同路标，指引着道路与方向.有效的问题情境可以提供丰富的学习材料和信息，有利于学生主动地探究和思考，有利于优化学生的认知结构，学生的学习策略.因此，在数学教学中，教师要精心设计有效的问题情境，使学生由情人境，情景交融，激起学生思维的浪花，把学生引人思考的境地.并有意识地为他们发现疑难、解决问题提供桥梁和阶梯，引导他们一步一步走向知识的殿堂，让学生的数学知识、数学方法和思维能力在“动态”中生成.