摘 要 实时调度算法是实时系统的关键。验证实时调度算法的可行性是在实时系统中实施某种调度算法的必经环节。本文针对硬实时调度算法中的最早时限优先(EDF)调度算法,分别介绍在简单模型上和复杂模型上如何判定实时任务的可行性。
关键词 实时;调度算法;可行性分析;响应时间
1 前言
硬实时调度算法,常见的分为速率单调调度法(RM)、 时限调度法(DM)和最早时限优先调度算法(EDF)。 EDF调度总是比固定优先级调度取得更高的利用率。相对于速率单调调度法(RM)和 时限调度法 (DM),EDF的时限是任意的,更适用于实际的实时系统。检查一组或一个具体实时任务是否能采用某种调度算法进行实时调度。这一过程叫调度算法的可行性判定。针对不同的算法,可行性测定有很多种。本文对常见的硬实时调度算法EDF介绍了相应的可行性测定方法。即假定任务同时启动,任务的最坏响应时间(即任务就绪到任务被完成的最长时间段)是否大于其任务时限,若大于,则调度可行,否则任务不可调度。在简单介绍完该方法后,对该方法进行了编程实现。
2 EDF简单实时模型的可行性测定
简单实时模型即各任务都是独立的周期任务,任务之间相互独立,无资源共享。Liu和Layland的
[2]不仅介绍了针对固定优先级调度的基于利用率的测试,而且也为最早时限优先级算法(EDF)给出了一个基于利用率的测试:只要进程集合(对于简单进程模型)的利用率 小于1,那么所有时限将能被满足。但这种测试方法的缺点是不准确,不适应于更一般的进程模型。
3 EDF的基于最坏响应时间的可调度性测试
所谓响应时间是指任务的某次释放到任务完成所花费的时间,而最坏响应时间是指所有响应时间中最长的响应时间。本文中介绍的方法——EDF的基于最坏响应时间的可调度性测试即是首先找出所给任务集的各个任务的最坏响应时间,然后将各个任务的最坏响应时间与相对时限相比较,如果所有任务的最坏响应时间都不大于各自的相对时限,那么该任务集可调度。如果没有通过测试,则该任务集不可调度。对调度的判断采用响应时间测试方法的优点之一是该方法适应于更一般的进程模型,优点之二它们是充分必要条件——如果任务集合通过测试,则可调度,否则,不可调度。可见找出最坏响应时间对于任务的可调度性的判断是非常重要的。下面介绍如何找出任务的最坏响应时间。EDF调度算法的最坏时间响应分析的基本思想: 所求任务i的最坏响应时间一定在处理器的忙碌期找到
[3]。可知任务i的最坏响应时间不一定在处理器的第一忙碌期找到,但它能在这样的忙碌期找到:在该忙碌期中,除了任务i外其它任务都在忙碌期的开始同时释放,然后各个任务按各自的周期而再次释放。 因为虽然任务同时释放的情况很特殊,但我们可以把其它任务都移到忙碌期的开始时刻后再同时释放,这种移动不但不会减少任务i的响应时间,相反可能增加其响应时间,而我们就是要求任务I的最坏响应时间,因此这样的移动是合理的。更有利于出任务的最坏响应时间。 设忙碌期的始端时刻为t1,结束时刻为t2。除任务i外的任务于忙碌期的开始时刻同时释放,任务i的相对时限为Di,设任务i的某次执行于时刻a释放,因此任务i的绝对时限为d=a+Di。在忙碌期内所有任务的绝对时限都小于或等于任务i的绝对时限,因此任务i的完成时刻即是忙碌期的结束时刻t。见图1。

图1为讨论方便,令t
1=0,那么任务i的响应时间即是L
i(a)-a。现在的问题就变成如何计算忙碌期的长度L
i(a)?忙碌期长度即是从时刻t1释放到时刻t2完成的任务的计算时间总和。所以L
i(a)=

C
j+δ
i(a,L
i(a))C
i [3] (1)
(其中,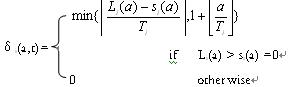 |
任务i的第一次释放时刻为
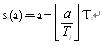
对于等式
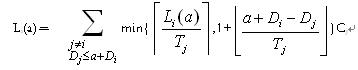
+δ
i(a, L
i(a))C
i可知,因为L
i(a)是未知的(它是正在计算的值),由于高限函数和低限函数,使方程难以求解。可构造一递推关系
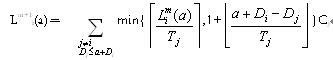
+δ
i(a, L
mi(a))C
i若令
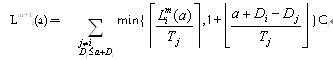
那么等式(1)变成 L
i(m+1)(a)=W
i(a, L
i(m)(a) ) (2) (其中
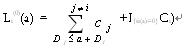
) 经过证明只要利用率
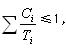
,那么递推式(2)就收敛,方程有解。这样当L
i(m+1)(a)= L
i(m)(a) ,方程的解L
i(a)就找到,就是L
i(m)(a)。求解过程我们可以用时间窗口的概念来一下求L
i(a)思路:我们可以将L
i(a)这段时间称为时间窗口(见图1),。那么在时间窗口内,只能有优先级高于或等于任务i(即绝对时限小于或等于任务I的时限d)的任务能执行,随着更多优先级的任务落入时间窗口,时间窗口的长度不断扩大,当没有更高优先级的任务需要执行时,则时间窗口到达最大,此时的时间窗口的长度即是忙碌期长度L
i(a)。 知道了 L
i(a)的表达式后,可以在忙碌期内让a取不同的值,通过不同的a值,计算出任务i不同的L
i(a)值,响应时间为r
i(a) = max{C
i,L
i(a)-a},从其中找出最大的r
i(a), 这就是所要求的最坏响应时间 r
i=max{r
i(a)} 上述方法对于判定任务集的可行性,相当有效。但由于计算响应时间的步骤多而且复杂,因此考虑用程序实现。程序c代码如下: /*首先定义一个实时任务结构体rt_task_struct,其成员T为实时任务的周期,成员D为实时任务的绝对时限,成员C为实时任务的最坏执行时间。*/typedef struct { int T; int D; int C; }rt_task_struct;main(void){/* 定义实时任务结构体数组rt_task[40],定义最大任务数为40*/rt_task_struct rt_task[20]; int tasknum,;/*本次待判定的任务数tasknum*/int r[40],ai[40];/* r[40]数组用来放置相应任务的最坏响应时间,ai[40]用来放置取得该响应时间时的时刻值*/ float L0=0,Ln1=0,Ln=0; float sia,I_sia; float Lm0=0,Lm=0,Lm1,ria; float w,delta,wm=0; float m1,m2,m3,m4; int i,j; scanf("%d",&tasknum);/*输入本次待判定的任务数*/ for(i=0;i<tasknum;i++) /*输入所有实时任务的周期、时限、最坏执行时间*/ { scanf("%d,%d,%d",&rt_task[i].T,&rt_task[i].D,&rt_task[i].C); } /* 最长忙周期Ln1,因为实时任务的最坏响应时间一定在最长忙周期中找到,利用公式
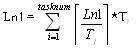
*/ for(i=0; i<tasknum; i++) L0=L0+rt_task[i].C; Ln1=L0; while(Ln1!=Ln) { Ln=Ln1; Ln1=0; for(i=0;i<tasknum;i++) Ln1=Ln1+(float)ceil(Ln/rt_task[i].T)*rt_task[i].C; } a_max=(long)Ln1;/*将不大于最长忙周期Ln1的最大整数赋给a_max*/ for(i=0;i<tasknum;i++) /*计算每个任务的最坏响应时间 */ { for(a=0;a<=a_max;a++) { sia=a-(float)floor((float)a/rt_task[i].T)*rt_task[i].T; if(sia==0) I_sia=1; else I_sia=0; for(j=0;j<tasknum;j++) { if(j==i || (rt_task[j].D>a+rt_task[i].D)) continue;/*如果任务j=i或者其时限D
j>a+D
i,则退出本次循环 */ Lm0=Lm0+rt_task[j].C; } Lm0=Lm0+I_sia*rt_task[i].C; Lm1=Lm0; while(Lm1!=Lm) { Lm=Lm1; Lm1=0;wm=0; if(Lm > sia) { m1=(float)ceil(Lm-sia/rt_task[i].T); m2=1+(float)floor((float)a/rt_task[i].T); delta=min(m1,m2); } else delta=0; for(j=0;j<tasknum;j++) { if(j==i|| (rt_task[j].D > a+rt_task[i].D)) continue; m3=(float)ceil(Lm/rt_task[j].T);m4=1+(float)floor(((float)a+rt_task[i].D-rt_task[j].D)/rt_task[j].T); wm=wm+min(m3,m4)*rt_task[j].C; } w=wm+delta*rt_task[i].C; Lm1=w; } ria=max(rt_task[i].C,Lm1-a); if(ria>r[i]) {r[i]=ria; ai[i]=a;} }printf("%f,%f,%f,%f,%f,%f/n",i,rt_task[i].T,rt_task[i].D,rt_task[i].C,r[i],ai[i]); }}下面举例说明: 例:假定实时系统中有如下4个任务,任务时间属性如表格1下所示(时间单位:毫秒):
| i | Di | Ti | Ci | |
| 1 | 4 | 4 | 1 | |
| 2 | 9 | 6 | 2 | |
| 3 | 6 | 8 | 2 | |
| 4 | 12 | 16 | 2 | |
表格1
| a=0 | r3(a)=3 |
| a=1 | r3(a)=2 |
| a=2 | r3(a)=2 |
| a=3 | r3(a)=2 |
| … | r3(a)=2 |
| a=8 | r3(a)=2 |
| a=9 | r3(a)=4 |
| a=10 | r3(a)=4 |
| … | r3(a |
表格2 由表格2可知任务3的最坏响应时间为r
3=4(表格2中的数据为任务3对应于不同a值时的响应时间)。 还可以按方法计算出其它任务的最坏响应时间:
| 任务i | 最坏响应时间 |
| a1=11 | r1=2 |
| a2=6 | r2=7 |
| a3=9 | r3=4 |
| a4=10 | r4=3 |
4 小结
实时调度算法的可行性分析是实时系统的关键技术,决定了实时系统的能否采用某种调度算法进行调度。本文采用了最坏响应时间的分析方法,即计算出系统中每个任务的最坏响应时间,然后判断每个任务的时限是否能满足条件,从而决定实时任务的可行性。
[1] M. Joseph, P. Pandya, "Finding Response Times in a real-Time System", The Computer Journal29 (5), 1986, pp.390-395.[2] C. Liu, J. Layland, "Scheduling Algorithms for Multiprogramming in a Hard-Real-TimeEnvironment", Journal of the ACM 20 (1), 1973, pp.40-61.[3]Marco Spuri,“Analysis of Deadline Scheduled Real-Time Systems”[4] B. Sprunt, L. Sha, J. Lehoczky, "Aperiodic Task Scheduling for Hard-Real-Time Systems",Real Time systems 1(1), pp.27-60, 1989
 图1为讨论方便,令t1=0,那么任务i的响应时间即是Li(a)-a。现在的问题就变成如何计算忙碌期的长度Li(a)?忙碌期长度即是从时刻t1释放到时刻t2完成的任务的计算时间总和。所以Li(a)=
图1为讨论方便,令t1=0,那么任务i的响应时间即是Li(a)-a。现在的问题就变成如何计算忙碌期的长度Li(a)?忙碌期长度即是从时刻t1释放到时刻t2完成的任务的计算时间总和。所以Li(a)= Cj+δi(a,Li(a))Ci [3] (1)
Cj+δi(a,Li(a))Ci [3] (1)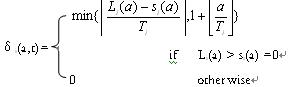
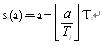
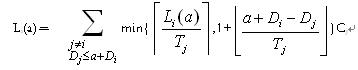 +δi(a, Li(a))Ci可知,因为Li(a)是未知的(它是正在计算的值),由于高限函数和低限函数,使方程难以求解。可构造一递推关系
+δi(a, Li(a))Ci可知,因为Li(a)是未知的(它是正在计算的值),由于高限函数和低限函数,使方程难以求解。可构造一递推关系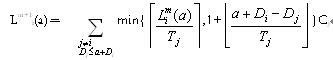 +δi(a, Lmi(a))Ci若令
+δi(a, Lmi(a))Ci若令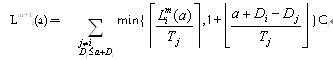 那么等式(1)变成 Li(m+1)(a)=Wi(a, Li(m)(a) ) (2) (其中
那么等式(1)变成 Li(m+1)(a)=Wi(a, Li(m)(a) ) (2) (其中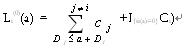 ) 经过证明只要利用率
) 经过证明只要利用率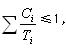 ,那么递推式(2)就收敛,方程有解。这样当Li(m+1)(a)= Li(m)(a) ,方程的解Li(a)就找到,就是Li(m)(a)。求解过程我们可以用时间窗口的概念来一下求Li(a)思路:我们可以将Li(a)这段时间称为时间窗口(见图1),。那么在时间窗口内,只能有优先级高于或等于任务i(即绝对时限小于或等于任务I的时限d)的任务能执行,随着更多优先级的任务落入时间窗口,时间窗口的长度不断扩大,当没有更高优先级的任务需要执行时,则时间窗口到达最大,此时的时间窗口的长度即是忙碌期长度Li(a)。 知道了 Li(a)的表达式后,可以在忙碌期内让a取不同的值,通过不同的a值,计算出任务i不同的Li(a)值,响应时间为ri(a) = max{Ci,Li(a)-a},从其中找出最大的ri(a), 这就是所要求的最坏响应时间 ri=max{ri(a)} 上述方法对于判定任务集的可行性,相当有效。但由于计算响应时间的步骤多而且复杂,因此考虑用程序实现。程序c代码如下: /*首先定义一个实时任务结构体rt_task_struct,其成员T为实时任务的周期,成员D为实时任务的绝对时限,成员C为实时任务的最坏执行时间。*/typedef struct { int T; int D; int C; }rt_task_struct;main(void){/* 定义实时任务结构体数组rt_task[40],定义最大任务数为40*/rt_task_struct rt_task[20]; int tasknum,;/*本次待判定的任务数tasknum*/int r[40],ai[40];/* r[40]数组用来放置相应任务的最坏响应时间,ai[40]用来放置取得该响应时间时的时刻值*/ float L0=0,Ln1=0,Ln=0; float sia,I_sia; float Lm0=0,Lm=0,Lm1,ria; float w,delta,wm=0; float m1,m2,m3,m4; int i,j; scanf("%d",&tasknum);/*输入本次待判定的任务数*/ for(i=0;i<tasknum;i++) /*输入所有实时任务的周期、时限、最坏执行时间*/ { scanf("%d,%d,%d",&rt_task[i].T,&rt_task[i].D,&rt_task[i].C); } /* 最长忙周期Ln1,因为实时任务的最坏响应时间一定在最长忙周期中找到,利用公式
,那么递推式(2)就收敛,方程有解。这样当Li(m+1)(a)= Li(m)(a) ,方程的解Li(a)就找到,就是Li(m)(a)。求解过程我们可以用时间窗口的概念来一下求Li(a)思路:我们可以将Li(a)这段时间称为时间窗口(见图1),。那么在时间窗口内,只能有优先级高于或等于任务i(即绝对时限小于或等于任务I的时限d)的任务能执行,随着更多优先级的任务落入时间窗口,时间窗口的长度不断扩大,当没有更高优先级的任务需要执行时,则时间窗口到达最大,此时的时间窗口的长度即是忙碌期长度Li(a)。 知道了 Li(a)的表达式后,可以在忙碌期内让a取不同的值,通过不同的a值,计算出任务i不同的Li(a)值,响应时间为ri(a) = max{Ci,Li(a)-a},从其中找出最大的ri(a), 这就是所要求的最坏响应时间 ri=max{ri(a)} 上述方法对于判定任务集的可行性,相当有效。但由于计算响应时间的步骤多而且复杂,因此考虑用程序实现。程序c代码如下: /*首先定义一个实时任务结构体rt_task_struct,其成员T为实时任务的周期,成员D为实时任务的绝对时限,成员C为实时任务的最坏执行时间。*/typedef struct { int T; int D; int C; }rt_task_struct;main(void){/* 定义实时任务结构体数组rt_task[40],定义最大任务数为40*/rt_task_struct rt_task[20]; int tasknum,;/*本次待判定的任务数tasknum*/int r[40],ai[40];/* r[40]数组用来放置相应任务的最坏响应时间,ai[40]用来放置取得该响应时间时的时刻值*/ float L0=0,Ln1=0,Ln=0; float sia,I_sia; float Lm0=0,Lm=0,Lm1,ria; float w,delta,wm=0; float m1,m2,m3,m4; int i,j; scanf("%d",&tasknum);/*输入本次待判定的任务数*/ for(i=0;i<tasknum;i++) /*输入所有实时任务的周期、时限、最坏执行时间*/ { scanf("%d,%d,%d",&rt_task[i].T,&rt_task[i].D,&rt_task[i].C); } /* 最长忙周期Ln1,因为实时任务的最坏响应时间一定在最长忙周期中找到,利用公式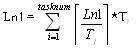 */ for(i=0; i<tasknum; i++) L0=L0+rt_task[i].C; Ln1=L0; while(Ln1!=Ln) { Ln=Ln1; Ln1=0; for(i=0;i<tasknum;i++) Ln1=Ln1+(float)ceil(Ln/rt_task[i].T)*rt_task[i].C; } a_max=(long)Ln1;/*将不大于最长忙周期Ln1的最大整数赋给a_max*/ for(i=0;i<tasknum;i++) /*计算每个任务的最坏响应时间 */ { for(a=0;a<=a_max;a++) { sia=a-(float)floor((float)a/rt_task[i].T)*rt_task[i].T; if(sia==0) I_sia=1; else I_sia=0; for(j=0;j<tasknum;j++) { if(j==i || (rt_task[j].D>a+rt_task[i].D)) continue;/*如果任务j=i或者其时限Dj>a+Di,则退出本次循环 */ Lm0=Lm0+rt_task[j].C; } Lm0=Lm0+I_sia*rt_task[i].C; Lm1=Lm0; while(Lm1!=Lm) { Lm=Lm1; Lm1=0;wm=0; if(Lm > sia) { m1=(float)ceil(Lm-sia/rt_task[i].T); m2=1+(float)floor((float)a/rt_task[i].T); delta=min(m1,m2); } else delta=0; for(j=0;j<tasknum;j++) { if(j==i|| (rt_task[j].D > a+rt_task[i].D)) continue; m3=(float)ceil(Lm/rt_task[j].T);m4=1+(float)floor(((float)a+rt_task[i].D-rt_task[j].D)/rt_task[j].T); wm=wm+min(m3,m4)*rt_task[j].C; } w=wm+delta*rt_task[i].C; Lm1=w; } ria=max(rt_task[i].C,Lm1-a); if(ria>r[i]) {r[i]=ria; ai[i]=a;} }printf("%f,%f,%f,%f,%f,%f/n",i,rt_task[i].T,rt_task[i].D,rt_task[i].C,r[i],ai[i]); }}下面举例说明: 例:假定实时系统中有如下4个任务,任务时间属性如表格1下所示(时间单位:毫秒):
*/ for(i=0; i<tasknum; i++) L0=L0+rt_task[i].C; Ln1=L0; while(Ln1!=Ln) { Ln=Ln1; Ln1=0; for(i=0;i<tasknum;i++) Ln1=Ln1+(float)ceil(Ln/rt_task[i].T)*rt_task[i].C; } a_max=(long)Ln1;/*将不大于最长忙周期Ln1的最大整数赋给a_max*/ for(i=0;i<tasknum;i++) /*计算每个任务的最坏响应时间 */ { for(a=0;a<=a_max;a++) { sia=a-(float)floor((float)a/rt_task[i].T)*rt_task[i].T; if(sia==0) I_sia=1; else I_sia=0; for(j=0;j<tasknum;j++) { if(j==i || (rt_task[j].D>a+rt_task[i].D)) continue;/*如果任务j=i或者其时限Dj>a+Di,则退出本次循环 */ Lm0=Lm0+rt_task[j].C; } Lm0=Lm0+I_sia*rt_task[i].C; Lm1=Lm0; while(Lm1!=Lm) { Lm=Lm1; Lm1=0;wm=0; if(Lm > sia) { m1=(float)ceil(Lm-sia/rt_task[i].T); m2=1+(float)floor((float)a/rt_task[i].T); delta=min(m1,m2); } else delta=0; for(j=0;j<tasknum;j++) { if(j==i|| (rt_task[j].D > a+rt_task[i].D)) continue; m3=(float)ceil(Lm/rt_task[j].T);m4=1+(float)floor(((float)a+rt_task[i].D-rt_task[j].D)/rt_task[j].T); wm=wm+min(m3,m4)*rt_task[j].C; } w=wm+delta*rt_task[i].C; Lm1=w; } ria=max(rt_task[i].C,Lm1-a); if(ria>r[i]) {r[i]=ria; ai[i]=a;} }printf("%f,%f,%f,%f,%f,%f/n",i,rt_task[i].T,rt_task[i].D,rt_task[i].C,r[i],ai[i]); }}下面举例说明: 例:假定实时系统中有如下4个任务,任务时间属性如表格1下所示(时间单位:毫秒):