摘  要  针对现有模糊Petri网的规则推理算法存在的不完善问题，提出并开发了优化的推理算法。该算法适用于大部分基于规则的推理系统，正确直观的仿真从出发命题开始到目标命题的推理过程。详细阐述了模型和算法，对具体的算例进行分析并与已有的算法进行比较突出其优点。    关键词  模糊Petri网；基于规则；推理；知识表示 

 

1  引言

    模糊Petri网(Fuzzy Petri Net，FPN)作为一种适合于描述异步、并行、模糊数据的机系统模型，被广泛的应用在基于规则的模糊推理系统中。伴随FPN的，相应模型的顺向推理算法以及逆向推理算法也在不断发展与完善。Looney最早给出了只适合于简单PN结构的顺向推理算法^[3]。其后，Chen又给出了具体且精确的FPN数学定义，并优化了原有算法^[1]。Li 等人提出了一种具有自适应能力的FPN^[4]，不但可以实现知识推理，同时具有类似神经的自我学习能力。

    我们发现，现有的这些算法对于较简单的模型结构比较有效，当推理系统对应的FPN模型具有较复杂的结构时，则存在一定的问题，譬如：

    (1)一些从始发命题到结论命题的推理路径并未充分考虑，如[1]。    (2)不适合并行推理，如文献[1][3]。    (3)对于一些库所，即使在推理中得到了它们的令牌值(Token)，但在后续过程中不能被涉及到，如文献[1]。    (4)在文献[4]中，当一个变迁被允许发生后，其输入库所全部被删除，这部分被删除掉的库所有可能包含了其它库所的输入库所，造成整个推理无法正常进行。    因此，文本在以往研究的基础上，提出一种更具有灵活性和适用性的基于模糊Petri网的顺向规则推理算法。

2  基于Petri网的模糊推理

    一个模糊Petri网包含两种节点：库所(Place)和变迁(Transition)。有向弧可以从库所指向变迁或从变迁指向库所。在图形表示中，库所由圆形节点表示，变迁由方形节点表示。将FPN应用于规则系统中，每条规则表示为一个变迁，该规则的前提命题和结论命题则表示为该变迁的输入库所和输出库所。每个库所都有可能包含令牌值(Token)用来描述该库所对应的命题的可信度(Degree of Truth)。每个变迁对应一个确信因子(Certainty Factor，CF)用来表述对应规则的确信度。实例一：假设有如下规则：    假如A is B，则C is D。    该规则包含一个前提命题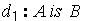和一个结论命题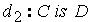，命题d₁,d₂用对应的库所P₁,P₂表示，规则用变迁t₁表示，则该规则可用如图1的FPN表述。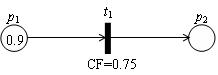图1  基于实例一规则的FPN    根据文献[1]中的定义，一个基于规则系统的FPN可以被定义为一个六维量：FPN=(P,T,I,O,F,W)。其中，    P={P₁,P₂,...P_n}为有限的库所集合，对应命题；    T={t₁,t₂,...t_n}为有限的变迁集合，对应规则；    I:T→P为映射变迁到其所有输入库所的输入方程；    O:T→P为映射变迁到其所有输出库所的输出方程；    F:T→[0,1]为映射变迁到其确信因子的方程；    W:P→[0,1]为映射库所到其令牌指的方程。    如果一个变迁 满足条件：对于任何P_s∈I(t_i)，有W(P_s)≥λ，λ为介于0和1之间的阈值，则该变迁将被点燃(Fired)，其输入库所的令牌值将被复制，并通过一定的点燃机制为该变迁的输出库所产生令牌值。    例如，根据FPN的定义，实例一中的规则可被规范化为FPN₁=(P,T,I,O,F,W)，其中P{P₁,P₂}，T{t₁}，I(t₁)={P₁}，O(t₁)={P₂}，F(t₁)=0.75，F(P₁)=0.9，F(P₂)=空。若令λ=0.5，则t₁点燃，根据图2的点燃机制，可得到输出库所P₂的令牌值为0.675。    当然，实际的规则不可能像实例一中那样简单，在其命题中有可能包含类似“与(AND)”或“或(OR)”连接符。我们将这样的组合式规则及其对应的模糊FPN结构归结为以下三种类型：图2   实例一的FPN点燃结果    类型一：假如命题1(d₁)与命题2(d₂)与 …… 与命题m(d_m)成立，则命题z(d_z)成立，CF=μ。对应FPN结构及点燃机制如图3所示。    类型二：假如命题1(d₁)成立，则命题a(d_a)与命题b(d_b)与 …… 与命题z(d_z)成立，CF=μ。对应FPN结构及点燃机制如图4所示。    类型三：假如命题1(d₁)或命题2(d₂)或 …… 或命题m(d_m)成立，则命题z(d_z)成立，CF=μ。对应FPN结构及点燃机制如图5所示。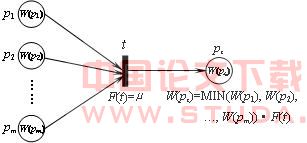图3  类型一FPN结构和点燃机制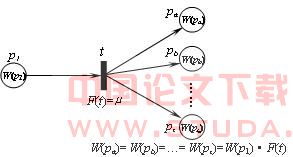图4  类型二FPN结构和点燃机制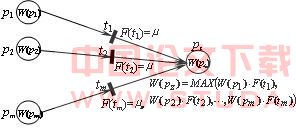图5  类型三FPN结构和点燃机制    令p_i,t_k为FPN中的任一库所和变迁，如果P_i∈I(t_k)，则称P_i是t_k的最近逆向库所(Nearest Backward Place，NBP)，变迁t_k所有的NBP的集合称为SNBP(t_k)。如果P_i∈O(t_k)，则称P_i是 t_k的最近前向库所(Nearest Forward Place，NFP)，变迁t_k所有的NFP的集合称为SNFP(t_k)。若存在流关系，从变迁t_k连向库所P_i，则称P_i为变迁t_k的向前库所(Forward Place，FP)，变迁t_S所有的FP集合称为 SFP(t_k)。    实例二：如图6所示的FPN结构中，每个变迁的SNBP，SNFP及SFP如表1所示。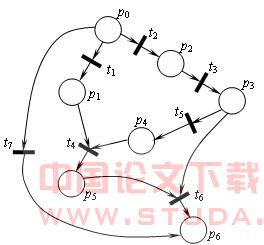图6 实例二中的FPN结构表1  实例二中每个变迁的SNBP，SNFP及SFP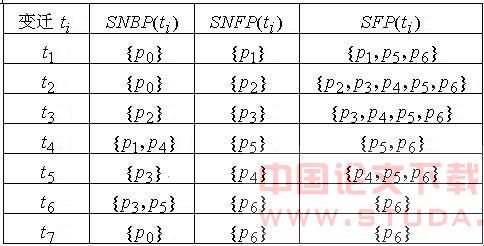3  基于Petri网的前向推理优化算法    本节将给出一个优化的基于Petri网的前向推理算法。首先引入下面几个定义：    定义1  种子库所(Seed Place)：对于一个FPN中的库所P_i，若不存在t_k，使得P_i∈SNFP（t_k），则P_i为种子库所。    在推理过程中，要求种子库所的令牌值是已知的或由用户给出。通常推理过程都是由种子库所开始，因此也被称为起始库所(Starting Place)。    定义2  目标库所(Goal Place)：在一个FPN中我们通过流推理最终得到其令牌值的库所。    定义3  节点(Node)：节点n_i=(P_i,W(P_i))，其中W(P_i)是库所P_i的令牌值。    定义4  已知节点集(Known Node Set，KNS)：若节点n_i中的库所P_i的令牌值已知，则n_i∈KNS。一个变迁点燃的前提条件是该变迁的SNBP能够在KNS中找到其对应的节点。    定义5  等待变迁集(Waiting Transition Set，WTS)：尚未被点燃，正待点燃的变迁集合。    定义6  未点燃变迁集(Un-Fired Transition Set，UFTS)：从未被点燃的变迁集合。    算法步骤：    输入：起始库所P_s及其令牌值W(P_s)。    输出：目标库所P_g及其令牌值W(P_g)。    (1)建立初始节点n_s=(P_s,W(P_s))，将n_s放入KNS。    (2)检测FPN中的所有变迁，若t_i满足P_g∈SFP(t_i)，则将t_i放入集合WTS中。    (3)将WTS中的元素复制到UFTS中，重复执行以下的循环，直到UFTS =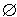。    对于所有t_i∈UFTS，执行以下操作：    if  SNBP(t_i) ⊆ KNS  then     {  t_i点燃；         产生节点n(p,W(p)) ，其中p∈SNFP(t_i) ，                    W(p)=MIN(W(SNBP(t_i)))．F(t_i)；         将节点n(p,W(p))放入KNS(如果KNS中已经存在节点n₀=(P₀,W(p₀))且p=P₀，若W(p₀)≤W(p)，则用节点n替代n₀，否则保持n₀；         将t_i从UFTS中删除。    }    else if  SNBP(t_i) 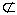KNS(令P_j,P_k,...,P_z)为属于SNBP(t_i) ，但不存在于KNS中的库所)    {  if  P_j,P_k,...,P_z  全部为种子库所 then       {  提示用户输入  W(P_j), W(P_k),...,W(P_z)；           t_i点燃；           产生节点n=(p,W(p))，其中p∈SNFP(t_i) ，                 W(p)=MIN(W(SNBP(t_i)))；           将节点n=(p,W(p))放入KNS(如果KNS中已经存在节点n₀=(P₀,W(p₀))且p=P₀，若W(p₀)≤W(p)，则用节点n替代n₀，否则保持n₀)；           将t_i从UFTS中删除。        }        else          将t_i加入WTS。     }    复制WTS 到UFTS；    将WTS置空。    (4)若存在节点n=(p_g,W(p_g))∈KNS，则输出p_g的令牌值。否则，输出结论：在起始库所p_s与目标库所p_g所对应的命题之间不存在因果关系。

4  具体实例

    用实例来对上节算法进行进一步阐述和校验。    实例三：令d₀,d₁,...,d₆为规则中的命题，在一个基于规则的系统中，包含以下模糊规则：    R1：IF d₀，THEN  d₁(CF = 0.90)；    R2：IF d₀，THEN  d₂(CF = 0.85)；    R3：IF d₂，THEN  d₃(CF = 0.95)；    R4：IF d₁  AND d₄，THEN d₅ (CF = 0.80)；    R5：IF d₃，THEN d₄ (CF = 0.90)；    R6：IF d₃  AND d₅，THEN  d₆(CF = 0.75)；    R7：IF d₀，THEN d₆ (CF = 0.90)；    根据以上规则，我们建立相应的FPN结构实际如图6所示，命题d₀,d₁,...,d₆用对应的库所 p₀,p₁,...,p₆表示，规则R1，R2，…，R7用对应的变迁t₀,t₁,...,t₇表示。设p₀为初始库所，W(p₀)=0.90，求W(p₆)。根据第三节的算法，具体推理步骤为：    由于p₆∈SFP(t_i)，i=1,2,3,4,5,6,7，则UFTS={t₁,t₂,t₃,t₄,t₅,t₆,t₇}，KNS={(p₀,0.90)}。    以下，进入DO-WHILE循环：    (1) t₁，由于SNBP( t₁)={p₀}⊆KNS， t₁点燃，生成节点(p₁,W(p₁))，其中W(p₁)= W(p₀)．F(t₁)=0.90．0.90=0.81。将节点(p₁,W(p₁))加入KNS，从UFTS中删除t₁。完成后：      UFTS={t₂,t₃,t₄,t₅,t₆,t₇}，WTS =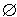 ，      KNS={(p₀,0.90),(p₁,0.81)}。    (2) t₂，步骤同 t₁相似。完成后：     UFTS={t₃,t₄,t₅,t₆,t₇}，WTS = 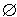，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77)}。    (3) t₃，步骤同t₁，t₂相似。完成后：     UFTS={t₄,t₅,t₆,t₇}，WTS = 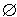，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73)}。    (4) t₄，由于SNBP(t₄)={P₁,P₄}，其中P₄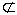KNS且P₄不是种子库所，所以将t₄加入WTS，从UFTS中删除t₄。完成后：     UFTS={t₅,t₆,t₇}，WTS = {t₄}，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73)}。    (5)t₅，步骤同t₁，t₂，t₃相似。完成后：     UFTS={t₆,t₇}，WTS = {t₄}，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73),(p₄,0.66)}。    (6)t₆，由于SNBP(t₆)={P₃,P₅}，其中P₅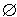KNS且P₅不是种子库所，所以将t₆加入WTS，从UFTS中删除t₆。完成后：     UFTS={t₇}，WTS = {t₄,t₆}，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73),(p₄,0.66)}。    (7)t₇，步骤同t₁，t₂，t₃和t₅相似。完成后：     UFTS=，WTS = {t₄,t₆}，     KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73),(p₄,0.66),(p₆,0.81)}。    (8)复制WTS到UFTS，则UFTS={t₄,t₆}，清空WTS。    (9) t₄，由于SNBP(t₄)={P₁,P₄}⊆KNS，t₄点燃，生成节点(p₅,W(p₅))，其中W(p₅)=MIN(W(p₁)),W(p₄)．F(t₄)=0.66．0.80=0.53。完成后：    UFTS={t₆}，WTS =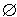，    KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73),(p₄,0.66),(p₆,0.81),(p₅,0.53)}。    (10)t₆，由于SNBP(t₆)={P₃,P₅}⊆KNS，t₆点燃，生成节点(p₆,W(p₆))，其中，W(p₆)=MIN(W(p₃)),W(p₅)．F(t₆)=0.53．0.75=0.40。由于KNS中已经存在p₆对应的节点(p₆,0.81)，且0.81>0.40，故保持原有节点。完成后：    UFTS=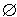，WTS =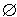，    KNS={(p₀,0.90),(p₁,0.81),(p₂,0.77),(p₃,0.73),(p₄,0.66),(p₆,0.81),(p₅,0.53)}。    至此，目标库所p₆的令牌值W(p₆)成功推出。

5  结论

    本文在现有算法的基础上，提出了一种基于模糊Petri网的规则向前推理优化算法。该算法避免了以往算法可能出现的不足，在一定程度上是对基于模糊Petri网的规则向前推理算法的一种完善。具有灵活性和适用性，对于较复杂的FPN结构也能成功的进行推理。

[1] S. M. Chen，J. S. Ke，J. F. Chang，“Knowledge Representation Using Fuzzy Petri Nets，” IEEE Trans. Syst. Man. Cybern.，Vol. 20，1990，pp. 311‑319. [2] M. M. Gao，M.C. Zhou，Y. Tang，“Intelligent Decision Making in Disassembly Process Based on Fuzzy Reasoning Petri Nets”，IEEE Trans. Systems，Man and Cybernetics，Part B，Vol. 34，no. 5，2004，pp. 2029-2034.[3] C. G.. Looney，“Petri Fuzzy Nets for Rule-based Decision Reasoning，” IEEE Trans. Syst. Man. Cybern.，Vol. SMC-18，1988，pp. 178‑183.[4] X. Li，F. Lara-Rosano，“Adaptive Fuzzy Petri Nets for Dynamics Knowledge Representation and Inference，” Expert System with Applications，Vol. 19，2000，pp. 235-241.[5] R. Yang，L.W.Shan，P. A. Heng，et al，“Improved Algorithm on Rule-based Reasoning Systems Modeled by Fuzzy Petri Nets”，Proc. 2002 IEEE Intern. Conf. Fuzzy Systems.