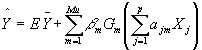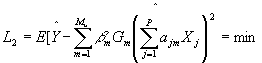流域年均含沙量的PP回归预测
摘要:应用投影寻踪回归技术,建立了流域年均含沙量的预测模型。用降雨量和年平均径流等4个因子建立的某流域平均含沙量的PPR预测结果的拟合合格率达100%,预留检验样本报准率为75%,表明PPR用于泥沙输移的预测研究是可行的。
关键词:流域 输沙量 投影寻踪回归 预测
1 引言
我国是一个水土流失严重的国家。严重的水土流失给工农业生产和国民建设造成巨大危害。产沙量是反映水土流失的一个重要指标。而气象要素、地形、土质状况、植被系统及人类活动均对产沙量有重要的影响。国内外不少学者针对不同的地域特征,对流域的产沙机理,泥沙输移规律及其防治对策等进行了大量的研究[1,2],但对诸多因子与产沙量之间的定量研究进行得较少。考虑到引起泥沙流失的诸多因子与产沙量之间的关系具有高维和非线性的特点,而传统的统计预报方法是采用“从某些假定出发,按照一定准则,找出最优拟合”这样一条途径,难以适应千变万化的客观世界,也就无法真正找出数据的内在规律。这种传统的预报方案往往是还原拟合较好,但预留实况检验的精度很差。近20年来,在统计学中提出了一条“审视数据,模拟,预报”称为探索性数据分析(EDA)新途径。本文正是采用基于这种新思路,应用投影寻踪回归技术(PPR),建立流域产沙量的多因子预报模型。
2 PPR原理及算法简介
投影寻踪是国际统计界70年代兴起的高新技术,是应用数学,统计学和机技术的交叉学科,属前沿领域。
PP是用来分析和处理高维数据,尤其是来自非正态总体高维数据的一类新兴统计方法[3]。其基本思想是:利用计算机技术把高维数据通过某种组合投影到低维子空间上,寻找出能反映原高维数据或特征的投影,在低维上对数据进行分析,以达到分析研究高维数据的目的。
传统的诸多线性模型通常局限于正态分布,但多数实际问题却不呈线性,因此勉强用线性手段进行辩识和预报,很难取得好的效果。而PP与其它非参数法一样,它可用来解决某些非线性问题。它虽然是以数据线性投影为基础,但它寻找的是线性投影中的非线性。因此,它可用来解决一定程度的非线性问题。PPR模型如下:设??X=(X1/:/:XP)是一P维随机向量,Y=f(X)?是一维随机变量,为了避免线性回归不能反映实际非线性情况的矛盾,PPR采用一系列岭函数的和来逼近回归函数的方法,即
| (1) |
式中Gm(Z)表示第m个岭函数,Z=(![]() )为岭函数的自变量,它是向量
)为岭函数的自变量,它是向量![]() 在
在![]() 方向上的投影,
方向上的投影,![]() 也为某方向的P维向量,M为岭函数的个数。
也为某方向的P维向量,M为岭函数的个数。
Friedman和Stuetzle提出了实现PPR的SMART多重平滑回归技术,SMART模型具有如下形式
?? | (2) |
它实际上是采用分层分组迭代交替优化方法对式(2)中的参数?α,β,Mu和岭函数Gm寻优。实现步骤为
①给定一个初始模型;
②把数据投影到一个低维空间上,找出数据与现有模型相差最大的投影,这就表明在这个投影中含有现有模型中没有反映的;
③把上述投影中所包含的并到现有模型上,得到改进了的新模型;
④再从这个新模型出发,重复以上步骤,直到数据与模型在任何投影空间都没有明显的差别为止。
模型的关键是最终估计出式(1)的参数:岭函数最优化项数Mu,岭函数Gm,系数αjm ,βm。?其判别准则仍是:选择适当的参数组合,使式
| (3) |
??具体作法是:把全体参数分成几组,除其中一组外,都给定一初值,然后对留下的一组参数寻优。得到结果后,把这一组参数的极值点作初值,另选一组参数在这一初值下寻优。多次重复直到参数收敛为止,即将?αjm,j=1,2…………P,βm及岭函数Gm划入一组,m=1,2,………M,共有M组。固定其中的M-1组,而对这一组ajm ,βm,Gm优化求解。此时,又将其分成三个子组,分别固定其中的两个子组,对第3子组优化。然后重复这一过程,直到收敛为止,即L2不再减小为止。
用SMART计算进行PPR计算时,实际操作十分简单,因为模型只有岭函数的光滑系数S,岭函数个数的上限M及最优个数Mu3个参数需要调整。光滑系数S确定着数据平滑窗口的大小,其取值范围S∈[0.1,0.9],考虑到在满足一定精度条件下,尽可能缩短模型运行时间,要求Mu≤M≤9,通常取下面这些组合:“M,Mu”为“5,3”;“6,5”;“6,4”和“9,6”等,其最佳值最终由计算结果分析确定。此外,样本容量值N可在不超过500范围内自行指定,屏显值与指定值N之差由程序自动视为预留检验样本数。PPR的理论分析及算法详见[4,5]。
3 某流域的年均含沙量的PPR回归预测
一般说来,流域的年均含沙量受多种因素影响,但对具体流域必须具体分析。其因子选择原则应尽可能选择那些与年均含沙量相关性好,而又比较稳定的有明确物理成因的因子作为PP回归建模因子。经分析,引起该流域含沙量增加的突发性偶然因素发生的可能性较小,年均含沙量比较稳定。该流域含沙量与气象、水文要素和下垫面植被状况关系密切。因此,选择了采伐面积?(X1),采伐量(X2),降雨量(X3)和年平均径流(X4)等4个因子作该流域产沙量的预报因子。
该流域的年均含沙量及有关的4个因子的监测数据见表1,数据取自[6]。
用PPR的SMART建立该流域年均含沙量的预测模型时,用表1中的前14组数据建模,后4组数据预留检验。将表1中全部18组数据输入PPR程序,在固定因子数P=4和建模样本数N=14情况下,反复调试模型中3个参数S.M和Mu的不同组合,使模型计算输出的拟合检验效果达最佳。由于式(2)中的岭函数Gm(Z)不是解析函数,而是数值函数表,因此,PP回归最终只给出达效果最佳时的模型参数组合值为S=0.1,M=6,Mu=4,此时年均含沙量的拟合和预留样本检验效果见表2。表2的后两行为4个预留样本检验结果。由于用PP回归计算的拟合值是多重平滑后的结果,因此,拟合值不是时序值,它与时序值有一个差异。不过这种拟合差异如用相对误差绝对值的平均值表示,不超过4%。用SMART计算实现该流域年均含沙量预测建模过程中,还同时给出如表3所示的各因子对年均含沙量的贡献大小的相对权值。这些相对权值就反映了这些因子对流域年均含沙量的影响程度。从表3可见,4个因子对年均含沙量影响从大到小依次是年径流量>降雨量>采伐面积>采伐量。
表1 某流域年均含沙量及有关因子实测值 |
Yearly average sediment concentration and measured data of related factors |
序号 | 年份 | 采伐面积 X1(M2) | 采伐量 X2(M3) | 降雨量 X3(mm) | 年平均流量 X4(m3/s) | 年平均含沙量 Y(kg/m3) |
1 | 1961 | 15100 | 29000 | 508.0 | 180 | 3.40 |
2 | 1962 | 20500 | 43350 | 453.7 | 141 | 3.00 |
3 | 1963 | 80000 | 92610 | 487.9 | 132 | 2.70 |
4 | 1964 | 91500 | 142775 | 572.3 | 182 | 3.37 |
5 | 1965 | 82500 | 2123160 | 455.7 | 113 | 6.894 |
6 | 1966 | 20000 | 227800 | 481.3 | 170 | 5.03 |
7 | 1967 | 17800 | 140000 | 541.3 | 199 | 3.55 |
8 | 1968 | 3900 | 15980 | 538.6 | 186 | 2.72 |
9 | 1969 | 17300 | 223200 | 460.6 | 99.8 | 4.05 |
10 | 1970 | 25700 | 229400 | 393.1 | 133 | 3.22 |
11 | 1971 | 49400 | 424500 | 373.9 | 106 | 2.65 |
12 | 1972 | 40700 | 561700 | 428.8 | 107 | 1.91 |
13 | 1973 | 77000 | 563600 | 482.1 | 140 | 3.00 |
14 | 1974 | 72900 | 557600 | 415.1 | 121 | 1.31 |
15 | 1975 | 63300 | 528300 | 536.7 | 144 | 2.33 |
16 | 1976 | 51600 | 488940 | 385.1 | 154 | 3.55 |
17 | 1977 | 60000 | 480500 | 412.2 | 111 | 3.35 |
18 | 1978 | 70000 | 530500 | 567.1 | 139 | 2.55 |
表2 年平均含沙量PPR模型拟合和预留检验结果 |
Results of fitting verification of yearly average concentration by using PPR model |
实测值 | 计算值 | 绝对误差 | 相对误差(%) | 实测值 | 计算值 | 绝对误差 | 相对误差(%) |
3.40 | 3.131 | -0.087 | -2.5 | 2.72 | 2.934 | 0.214 | 7.9 |
3.00 | 2.738 | -0.262 | -8.7 | 4.05 | 3.996 | -0.054 | -1.3 |
2.70 | 2.659 | -0.041 | -1.5 | 3.22 | 3.214 | -0.006 | -0.2 |
3.37 | 3.400 | 0.030 | 0.9 | 2.65 | 2.628 | 0.022 | -0.8 |
6.894 | 6.926 | 0.032 | 0.5 | 1.91 | 2.135 | 0.225 | 11.8 |
5.03 | 4.729 | -0.301 | -6.0 | 3.00 | 2.987 | -0.013 | -0.4 |
3.55 | 3.826 | 0.276 | 7.8 | 1.31 | 1.319 | 0.009 | 0.7 |
2.33 | 2.461 | 0.131 | 5.6 | 3.35 | 2.780 | -0.570 | -17.0 |
3.55 | 2.869 | -0.681 | -19.2 | 2.55 | 4.305 | 1.755 | 68.8 |
拟合合格项数:14 拟合率:100% 预留检验合格项数:3 合格率:75% | |||||||
表3 各因子的相对权值 |
Relative weighted values of factors |
权序 | 1 | 2 | 3 | 4 |
因子 | X4 | X3 | X1 | X2 |
相对权值 | 1.00000 | 0.85190 | 0.71617 | 0.29765 |
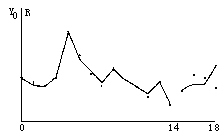
若以相对误差?δ<20%?算合格,从表2可见,年均含沙量PPR预测模型拟合样本数为全部合格,其拟合合格率为100%,而预留4个检验样本合格率为75%,其拟合和预留检验效果如图1所示。
应用PP回归技术建立该流域的年均含沙量预测模型的拟合精度较高,但预留的4个检验效果不太理想。这是因为流域年均含沙量除了受上述几个比较稳定的关系密切的因子影响外,也会受到某些突发性偶然因素比如特大暴雨,滑坡等灾害事故及人为因素的影响。而用PP回归建模时,无法考虑这些偶然因素作用。第18个预测值与实况值相差较大,有可能就是某些突发性因素影响的结果。 4 结论 |
|
1.PP回归采用了“审视数据—模拟—预测”探索性数据分析新途径,建立的模型稳健性和抗干扰性好,因而预测模型有较高的精度。
2.PP回归无论对于正态或偏态分布,线性或非线性,独立或非独立分布的数据都能有效地处理。因此,它适用于分析和处理流域含沙量等非正态和非线性等有关问题。
3.PP回归用于流域输沙量等预测建模,只需直接使用原始监测数据,不需要对数据作预处理,避免了人为干预,客观性好。
4.PP回归也可用于水土流失中其它指标的预测建模。
5.本文用PP回归技术建立了流域年均含沙量的预测模型,?求得年均含沙量S后,只要将年径流量QT×年均含沙量S就可得到流域的年输沙量QsT。?
6.本文用PP回归建立的流域年均含沙量预测模型未考虑对含沙量有影响的突发性因子在内,只适用于对含沙量有稳定影响因素的预测建模,如何把这些影响考虑在内,还有待进一步研究。
参 考 文 献
1 陈浩。学报。1992,6(2):17-23.
2 张醒。泥沙研究。1991,(1):15-19.
3 Friedman J.H.&. Stuetzle W.,J. Amer. Statis. Assoc. 1981, 76:817.
4 Huber P.J..Ann. Statistics, 1985,13:435.
5 郑祖国。水文。1994,(4):6-10.
6 吴建明编著。环境统计学。北京:环境出版社,1991:504.