摘  要  在统计自仿射模型中，分形维度和Hurst指数之间存在着线性关系。但也有很多统计模型允许分形维度和Hurst指数的任意组合。所以，判断那种模型更符合实际问题是十分必要的。本文对四组实际的以太网流量序列的分形维度和Hurst指数做了实验分析，并得出流量数据应采用分形维度和Hurst指数相分离的模型的结论。     关键词  自相似；长相关；分形维度；Hurst指数；估计  

1 引言

    如果一个随机信号x(t)的统计特性是自相似的（过程x(ct)和c^H x(t)具有相同的有限维联合分布），即它在被放大或缩小时其统计特性不变，则它被称为（统计）自相似的，也称为随机分形。若该随机信号x(t)具有平稳的增量，则称x(t)是一个具有平稳增量过程的自相似过程（H-sssi）。当0 < H < 1时，高斯H-sssi过程称为分数布朗运动（Fractional Brown motion, FBM）。若0.5 < H < 1，则序列具有长相关性（Long Range Dependence, LRD）。对FBM过程周期地进行采样然后一阶差分，可以得到分形高斯噪声（Fractional Gaussian Noise, FGN），它是一个平稳序列。实际的网络流量表现出长相关性，Hurst指数H是描述业务长相关性的重要参数，FGN是目前最为广泛的一种网络流量自相似模型^[1,2]。    数学家Hausdoff在1919年提出了连续空间的概念，也就是空间维数是可以连续变化的，它可以是整数也可以是分数，称为Hausdoff维数，即分形维度，记作D。它在一般情况下是一个分数。FBM的分形维度D与它的Hurst指数H之间满足以下关系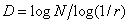             （1-1）    其中N为分形数，r为分形成线段的尺寸比例。当0 < H < 1时，D = 2-H。    实际工作中，D和H这两个参数都是十分重要的，从而值得研究下列的问题：（1）对于实际以太网网络流量而言，是否满足D = 2-H？（2）是否存在更符合实际的以太网网络流量的统计模型？本文针对这两个问题，结合实际以太网流量数据对D和H的关系做出进一步的论述。    所采用的四个实际以太网流量数据序列是美国Bellcore的研究人员采集的。数据序列的名称分别为pAug89.TL、pOct89.TL、Oct89Ext.TL和Oct89Ext4.TL^[3]。我们将对这四组数据的D和H分别做出估计，并对结果进行分析。

2  自相似随机过程模型

    平稳高斯随机过程x(t)，它的自相关函数为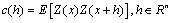：     （2-1）    当h→0时，自相关函数有如下的渐近形式  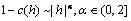          （2-2）    它表现了x(t)的局部特性，可以定义分形维度为：D = 2-α/2。如果在延时很大的时候，它的自相关函数c(h)是呈幂级数形式缓慢衰减，即当|h|→∞时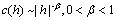，               （2-3）    它表现了x(t)的全局特性，即长相关特性。可以定义Hurst指数为：H = 1-β/2。FGN是一个平稳自仿射随机过程，它的自相关函数为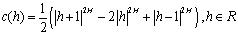：   （2-4）    此时H∈(1/2， 1)。对于一个自仿射模型，局部特性可以完全由全局特性反应出来，所以D和H间存在着线性关系，D = 2-H。    相对于上面介绍的自仿射模型，这里给出一种D和H相分离的统计模型——柯西类模型^[4]。这类模型的自相关函数可以表示为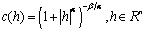：       （2-5）    自相关函数可以是α∈(0，2]和β ＞ 0的任意组合。如果β ＞ 0，c(h)在h→0和|h|→∞时的渐进性满足（2-2）、（2-3）式。因此，随机过程的分形维度D和Hurst指数H就可以分别由α和β计算出来。还有一些其它D和H相分离的统计模型，这里就不详细介绍了。

3  研究思路

3.1 经验变量图法（Empirical Variogram）估计分形维度D^[4,5]

    如果一个随机过程Z(x)的增量过程I_h = {Z(x) -Z(x + h): x∈Rⁿ}对所有的延时向量h都是平稳的，那么Z(x)就被称为固有平稳的，它的变量图（variogram）可以定义为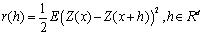：    （3-1）    增量h和变量图r(h)之间存在着如下的尺度关系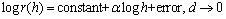：    （3-2）    当上面的尺度关系应用在平稳随机过程中时，这个平稳随机过程的自相关函数就满足（2-2）式。我们将r(h)和h画在双对数图(log-log plot)中，用最小二乘法做直线拟和，所拟和直线的斜率为α。

3.2 用小波法（Wavelet Method）估计Hurst指数^[6]

    小波法在时域和频域都可以使用，以离散小波变换和多分辨率分析（Multi-resolution Analysis）为基础，将序列x(t)分为近似值（低频部分）和细节（高频部分），分别用a_x和d_x表示。可以通过线性分析，在半对数图中计算H值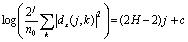       (3-3)    上式中，n₀是数据长度，c是有限常数。

4  实验结果与讨论

    我们选取pAug89.TL、pOct89.TL、Oct89Ext.TL和Oct89Ext4.TL四组长度N＝524288的真实以太网流量数据。分别对这四组数据估计它们的分形维度和Hurst指数。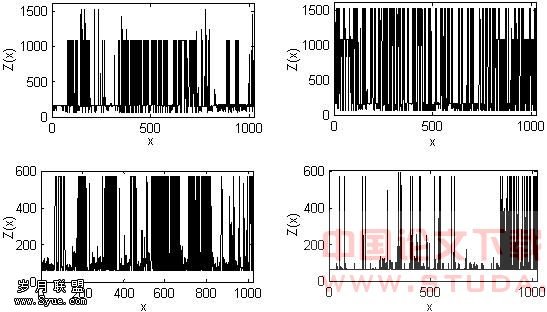
      图1  真实的以太流量数据pAug89.TL、pOct89.TL、Oct89Ext.TL和Oct89Ext4.TL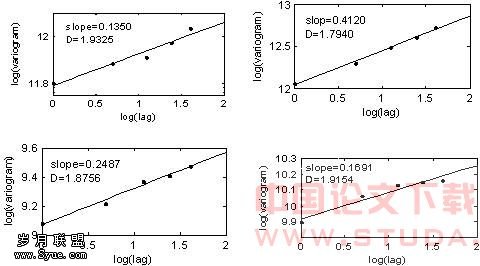

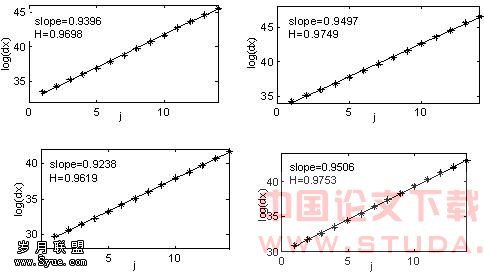      图2  用经验变量图法对四组数据估计的分形维度      图3  用小波法对四组数据估计的Hurst参数
    我们将这四组数据的D和H的值以及它们的和列于表1。我们可以从实验数据中得出，对于自仿射统计模型中的分形维度和Hurst指数之间存在D = 2-H的结论与实际的以太网流量数据是不相符合的，而柯西类模型中相分离的分形维度和Hurst参数则能更好的拟合以太网网络流量的真实统计特性。
表1  四组数据的分形维度、Hurst指数及二者之间的关系

	pAug89.TL	pOct89.TL	Oct89Ext.TL	Oct89Ext4.TL
分形维度D	1.9325	1.7940	1.8756	1.9154
Hurst指数H	0.9698	0.9749	0.9619	0.9753
D + H	2.9023	2.7689	2.8375	2.8907

5   结语

    本文简单的介绍了分形高斯噪声的两个重要参数——分形维度D和Hurst指数H，并且给出了分形高斯噪声自相关函数的两种不同的统计模型——D和H线性相关的统计模型和D和H分离的统计模型模型（柯西类模型）。通过对实际网络流量数据的分析，我们可以得出这样的结论：对于真实的以太网流量而言，分形维度和Hurst指数之间是两个独立影响随机序列统计特性的变量。所以（2-5）式的自相关函数模型更适合实际的问题。

1 W. E. Leland, M. S. Taqqu, W. Willinger, and D. V. Wilson, On the self-similar nature of Ethernet traffic (extended version)[J]. IEEE/ACM Transactions on Networking, 2 (2) 1994, 1-152 M. E. Crovella and A. Bestavros, Explaining World Wide Web Traffic Self-Similarity, Technical Report TR-95-015, October 12, 19953 Ming Li, W. Zhao, W. Jia, D.-Y. Long, and C.-H. Chi, Modeling autocorrelation functions of self-similar teletraffic in communication networks based on optimal approximation in Hilbert space[J], Applied Mathematical Modelling, 27 (3) 2003, 155-1684 Tilmann Geniting, Martin Schlather, Stochastic Models That Separate Fractal Dimension and Hurst Effect[J], SIAM review(Print) 46:22, 2004, 269-2825 Tilmann Gneiting. Zoltán Sasvári Martin Schlather, Analogies and Correspondences Between Variograms and Covariance Functions. NRCSE. Technical Report Series. NRCSE-TRS No. 056. October 12, 2000, 617-6306 G. W. Wornell, Wavelet-Based Representations for the 1/f Family of Fractal Processes[J], Proceedings of The IEEE, 81 (10) 1993