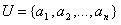摘  要   本文就目前Rough集直接处理不完备信息系统的Rough集模型进行讨论、归纳与，有利于对不完备信息系统的Rough集扩充方法的认识，对在不完备信息系统下拓展Rough集有所启示和。     关键词  不完备信息系统； Rough集；模型拓展1  引言    由Pawlak等人在20世纪80年代提出的经典Rough集理论在知识获取方面取得了很大的成功。但遗憾的是在传统的Rough集理论中，存在一个明显的假设，即所有可以获得的个体对象由这个属性集合给出完全描述。换句话说，用 表示个体对象集合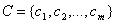， 表示属性集合，则对于任意 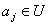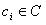， ，属性值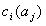 总是存在的，即 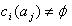。这个假设虽然是合理的，但是与很多现实情况有差异。在这些情况下，由于不可能得到一部分属性值，或者有些对象的某个属性值是肯定不可能得到的，这导致关于对象集合U 的描述是不完全的。因此，就导致了不完备信息系统的出现。然而，对不完备信息的理解存在两种语义解释，遗漏（missing）语意和缺席（absent）语意。遗漏语意下，认为遗漏值（或空值）将来是可以得到的并且可以与任意值相比较；而缺席语意下，认为缺席值（或空值）是无法再得到的，不能与任意值相比较。    为了使Rough集理论能适应于对不完备信息系统的处理，目前主要有两类方法。一是间接处理方法，这种方法有两种情形：第一种情形是删去带有缺失值的实例，但是将会丢失数据中很多有用的知识；第二种情形是通过一定的方法（通常是基于概率统计）把不完备信息系统转化为完备信息系统，即数据补齐，但是，补齐处理只是将未知值补以我们的主观估计值，或多或少改变了原始的信息系统，因此不一定完全符合客观事实。二是直接处理方法：其特点是对经典Rough集理论中相关概念在不完备信息系统下进行适当扩充。本文就直接处理方法目前的情况进行阐述与总结，有利于对不完备信息系统的Rough集扩充方法的认识，对在不完备信息系统下拓展Rough集有所帮助和参考。

2  不完备信息系统的扩充方法

2.1 容差关系

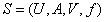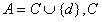    基于遗漏（missing）语意，Kryszkiewicz给出了容差关系的定义。给定信息系统 ，其中 是条件属性集合，d 是决策属性，对于具有空值的属性子集 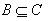，记空值为“*”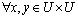， ，容差关系 T 定义如下：    定义2.1.1  容差关系 T 定义为：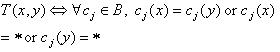

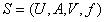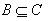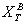    显然，T 是自反且对称的，但不传递。进一步，用符号 表示在属性集合 B 上满足关系 T(x,y) 的个体对象y的集合，即对象x 的容差类。根据定义2.1.1得到上、下近似的定义：    定义2.1.2　不完备信息表 中对象集合X 关于属性集 的上近似 和下近似 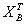分别定义为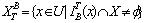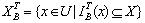：    ， 。    容差关系是目前面向不完备信息系统中应用最为广泛的一种Rough集扩充模型，它将缺失值的可能范围最大化，从而保证了后续算法可以挖掘到尽可能多的知识。但这种最大化的前提假设也同时增加了后续算法的难度和复杂度，在数据量较大，缺失值较多的情况下难以应用。

2.2 非对称相似关系

    Stefanowski和Tsoukias认为空值不是不确定的，而是当前不存在的，从而不允许比较空值，即缺席（absent）语意。基于这种观点他们给出非对称相似关系如下：    定义2.2.1　给定信息系统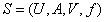 ，其中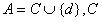 是条件属性集合，d 是决策属性，对于具有空值的属性子集 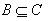，记空值为“?”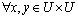， ，非对称相似关系S 的定义为: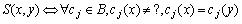

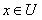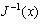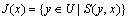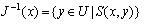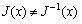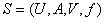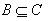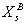    显然，S 是自反且传递的，但不对称。实际上，非对称相似关系可以认为是包含关系的一个代表，因为只要 x  的描述包含在 y 的描述中，就认为 x 与 y 相似。对于任意对象 ，可以定义两个非对称相似集合：    定义2.2.2  非对称相似于 的x 对象集合 J(x) ，x 与之非对称相似的对象集合 的定义为：，。      一般地， 。因此，    定义2.2.3　不完备信息表 中对象集合 X 关于属性集 的上近似 和下近似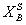 分别定义为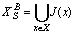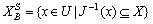： ， 。    这种关系乍看起来似乎有点奇怪，但我们总是认为孩子象父母，复制品象真品，反过来人们难于接受。如果系统环境如此，非对称相似关系是合理的。

2.3  量化容差关系

    为了进一步刻画容差关系和非对称相似关系中两个实例之间的“相似”程度Stefanowski和Tsoukias在研究了容差关系和非对称相似关系后提出了量化容差关系。    人们可以用不同的比较规则来定义不同的量化容差关系。给定一个量化容差关系，对于个体对象全集U中的每个元素，Stefanowski和Tsoukias定义了“容差类”概念。容差类是一个用关于元素的“容差度”作为成员函数的模糊集。如果容差度的值为1，量化容差关系就变成容差关系。事实上，容差关系是量化容差关系的特殊情形。在Stefanowski和Tsoukias提出的量化容差关系中，需要预先知道信息系统中属性值的概率分布情况，这对于一个新的不完备信息系统来说是很困难的。

2.4  特征关系

    Kryszkiewicz基于遗漏（missing）语意提出了容差关系，Stefanowski和Tsoukias基于缺席（absent）语意提出了非对称相似关系。然而，在实际应用中经常的情况是在一个不完备信息系统中遗漏（missing）语意和缺席（absent）语意同时存在，使用上述模型进行处理将出现困难。于是，J.W.Grzymala-Busse提出了特征关系。    假设在遗漏（missing）语意下的属性值表示为”*”，而在缺席（absent）语意下的属性值表示为”?”，J.W.Grzymala-Busse定义了如下的特征关系R:    定义2.4.1  给定信息系统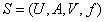 ，其中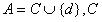 是条件属性集合，d 是决策属性，对于具有空值的属性子集 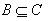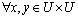， ，特征关系R定义如下：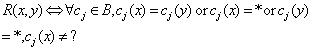

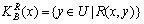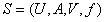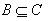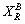    显然， R 是自反的，但是不对称和传递，并且容差关系 T 和非对称相似关系 S 是特征关系 R的特殊情形。进一步，用符号 表示在属性集合 B上满足关系 R(x,y)的个体对象 y 的集合，即 。根据定义2.4.1 得到上、下近似的定义：    定义2.4.2　不完备信息表 中对象集合X 关于属性集的上近似 和下近似 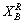分别定义为：(有三种形式)    第一种形式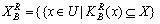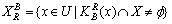： , 。    第二种形式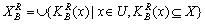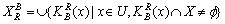： ， 。    第三种形式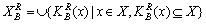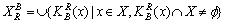： ， 。    对于完备信息系统来说，这三种形式的定义是等价的。但是，对于不完备信息系统，情况就不是如此，应该根据实际情况进行选择。

3  结束语

    应用Rough集理论直接处理不完备信息系统的首要任务就是构建在不完备信息系统下的Rough集模型，只有模型恰当，通过属性约简和规则约简得到的决策规则才能更加简约，与实际更加符合。本文通过对目前不完备信息系统Rough集模型的归纳、分析和，有利于对不完备信息系统下Rough集模型扩充方法的理解与认识，对在不完备信息系统下拓展Rough集模型有所帮助和参考。

参考

    [1]J.Stefanowski, A.Tsoukias. Incomplete Information Tables and Rough Classification. Computational Intelligence, 2001,Vol.17,3:545-566.    [2]M.Kryszkiewicz. Rough Set Approach to Incomplete Information Systems. Information Sciences, 1998,112:39-49.    [3]J.W.Grzymala-Busse. Rough Set Strategies to Data with Missing Attribute Values. Procedings of the Workshop on Foundations and New Directions in Data Mining, associated with the IEEE International Conference on Data Mining, Melbourne, FL, USA, 2003,11:56-63.    [4]R.Latkowski. Flexible Indiscernibility Relations for Missing Attribute Values. Fundamenta Informaticae, 2005,67:131-147.    [5]李仁璞,黄道. 基于RS理论的不完备信息系统处理方法. 华东理工大学学报, 2005,vol.31(2),4:227-231.    [6]王国胤. Rough集理论在不完备信息系统中的扩充.机研究与,2002,39(10):1238-1243.    [7]杨小平. 基于相似度的限制容差关系改进. 计算机工程与应用, 2005,29:97-99.