摘  要  针对基于认证证书的数字签名方案中公钥集中保存，系统容易受到主动攻击的缺点，提出了一种新的基于公钥自证明的认证加密方案。该方案中用户匿名注册，并获得由用户与CA共同产生的公钥证明，可以根据用户公钥证明推导其公钥；通信双方的公钥认证与消息签名结合在一起，由消息接收者在认证签名、恢复消息时完成公钥认证，因而减少了存储空间、通信量和量。      数字签名 公钥证书认证加密 公钥自证明  

1 前言

    随着计算机和通信技术的迅速，数字签名在商务、身份认证等方面广泛应用。数字签名通常是指签名者使用私钥对给定的消息签名，而验证者使用签名者的公钥验证签名。为了保证签名者所公布公钥的可靠性，一些学者们提出了基于证书的认证加密方案^[1,2]。假定有一个可信任的第三方CA为其用户颁发公钥证书，签名者用私钥对消息签名，验证者验证签名要进行两次签名验证：第一，利用签名者公钥证书中的公钥验证对消息的签名，第二，验证CA对签名人公钥证书的签名。由于用户的公钥保存在一个权威认证机构的公开密钥目录中，系统很容易遭到主动攻击和假冒攻击，而且CA的网络处理能力也成为制约系统效率的一个“瓶颈”。    针对这一安全隐患，Shamir^[3]于1984年提出了基于标识(ID)的密码体制思想。在该密码体制中，用户的标识用作公钥，因此用户的公钥不需要单独的认证证书。但是，该方案中用户的私钥由系统提供的，系统能够冒充用户。Girault^[4]于1991年提出自证明公钥的方案，有效解决了认证中心假冒用户地问题。在此方案中，认证中心使用系统的私钥为用户的标识签名，任何用户都能够从签名中推导出用户的公钥，用户的公钥不需要单独的认证证书。与基于标识的认证加密体制相比，自证明密码体制大大减少系统存储空间和计算量，且用户自己选择密钥，认证中心不知道用户的私钥，无法冒充用户，具有更高的安全性。一些学者^[5,6,7]对公钥自证明密码体制进行了大量研究，将公钥自证明方案沿用到了电子选举、电子商务等领域。    本文基于Girault自证明公钥的原理，提出了一种新的基于公钥自证明的认证加密方案。该方案中，接受者不需要保存用户的公钥，传送消息之前不需要进行公钥的自证明，消息接收者在恢复消息、验证签名的过程中实现对签名者的身份认证；签名者者不需要发送原消息，只有特定的接收者才能接收签名并恢复消息。而且，认证中心使用私钥为用户公钥签名，避免攻者冒充认证中心伪造公钥签名。

2 方案描述

2.1 系统初始化阶段

    在系统初始化阶段，认证中心（CA）负责生成系统参数。CA首先选择两个大素数p和q，使p=2p^’ +1和q=2q^’+1，其中p^’ 和q^’也是素数，然后计算n＝p*q，及其欧拉函数 φ(n)=（p-l）(q-1)。然后选择一个随机整数e，l<e< φ(n)，gcd(e,φ(n) =1, 并计算 d，使得ed=1 mod φ(n) ,接着CA选择一个整数g，g是n＝p*q的基元。还公布一个单向hash函数h( )。    CA的秘密参数：p、q、p^’ 、q^’、φ(n) 以及d，    CA的公开参数：e、n 、g和h( )。

2.2 用户注册阶段

    为了使向CA注册的用户获取的公钥证书，而CA不知道用户的私钥，因此用户公钥的分发不能简单地由CA 产生颁布。同时也为了用户身份的匿名要求，对CA也不能暴露，因此公钥证书的产生要由用户与CA共同协商完成。把这个注册过程称之为用户注册协议。    步骤1：用户U_A计算h_A＝h(ID_A)，其中ID_A代表U_A的身份标识，且对CA保密，U_A以匿名的身份h_A向CA提出注册申请；    步骤2：CA检查核实用户h_A的身份，若h_A通过身份检查，则CA计算r_A = g^-d mod n,将 r_A 传送给U_A；    步骤3：U_A 收到r_A  后，任选一个随机数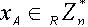 作为私钥，计算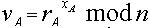，将v_A传送给CA；    步骤4：CA计算 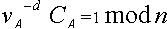，则将C_A 作为CA颁发的公钥证书，并将C_A传送给U_A；    步骤5：U_A 接收到U_A 发送的C_A后，计算 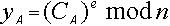，同时验证等式 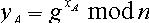是否成立，若成立，则证明在传输过程中参数未被篡改，C_A是CA的有效公钥签名。否则，签名无效。    上述注册过程，只有CA才能颁发U_A的公钥的证明。因为在注册过程中，CA使用私钥对U_A在协议交互过程中产生的一些特定信息进行签名，任何人若不知道CA私钥，是无法伪造的，其安全性程度高。如果攻击者企图获取U_A的私钥。那么他将面临求解离散对数的困难。如果攻击者企图伪造CA的公钥证明。那么他将面临求大素数的因子分解的困难。

2.3 签名生成阶段

    假定用户U_A 对消息M的签名，并将签名的消息传递给指定的接收者U_B。消息M签名生成过程如下：    步骤1：U_A 向U_B发送要进行签名的请求，并将C_A, h_A 传送给U_B；    步骤2：U_B 接收到U_A的签名请求，将C_B 传送给U_A；    步骤3：U_A 接收到U_B 发送的C_B后，计算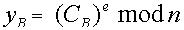  ,然后选择一个随机数k，进行数字签名：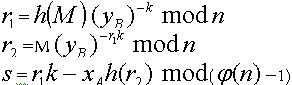

    步骤4：U_A将对消息M的签名（r₁ ,r₂ , s）送给U_B。

 

2.4 消息恢复验证阶段

    U_B接收到消息M的签名（r₁ ,r₂ , s）后，恢复消息M，并对恢复的消息M进行验证。恢复并验证消息的过程如下：    步骤1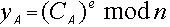：  ；    步骤2：恢复消息等式 

；      

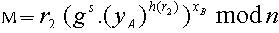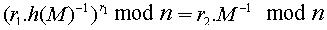    步骤3：验证消息等式 ，若消息验证等式成立，则接受这次签名。    这个消息恢复验证的过程同时也实现对U_A和U_B身份的双向认证。如果消息是U_A的签名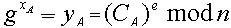，，则U_B使用U_A的公钥验证签名，并用自己的私钥解密恢复消息，实现双向的身份认证。消息恢复等式的正确性证明如下：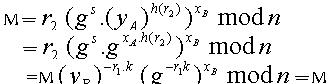

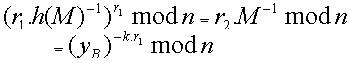
    同时如果U_B恢复的消息M 是正确，则有消息验证等式成立：

3  安全性分析

    （1）攻击者不可能伪造CA的公钥签名。CA为用户U_A的公钥签名时使用了私钥。任何攻击者不知道U_A的公钥是不可能伪造CA的签名。因为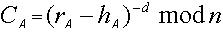，只有CA拥有私钥，能产生有效的公钥证明。而攻击者要想获取CA的私钥，将面临大素数的因子分解困难。CA可以伪造公钥证明，但一个用户有两个合法的公钥证明，则证明CA的不可信赖性。    （2）攻击者在不知道U_A的私钥 的情况下，伪造一个合法的签名是的不可能性。攻击者必须计算用户的私钥X_A ，并且截获U_B的公钥的证明C_B，才能假冒U_A进行签名。而攻击者要想获取U_A的私钥X_A，将面临求解离散对数的困难。    （3）攻击者截取签名（r₁ ,r₂ , s）后，要试图获取消息是不可能的。因为攻击者不知道接收者U_B的私有密钥x_B，因此他无法根据消息恢复方程求解得到M。也就是说只有指定的消息接收者U_B才可能求解得到M，他与消息发送者之间的相互确认是通过用户公钥的自认证协议实现的。   （4）消息密钥 K 可以多次使用。对于不同的消息M和M，使用相同的消息密钥 K ，产生两个消息签名（r₁ ,r₂ , s）和（r₁ ,r₂ , s^'）由于不同的消息产生的r_1、 r₂  和s 都不相同，攻击者不能根据签名等式 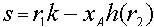分析得出签名者的私钥 。

4 方案的比较

    本文所提出的基于公钥自证明的认证加密方案是根据Girault的公钥自证明原理，在Tseng yuh-Min等人的自证明方案的基础上进行设计的，同时根据[7]中对Tseng yuh- Min方案的缺点分析，提出的一种更安全的公钥自证明方案。    首先，本方案中，CA对用户的公钥签名时有效引入CA的私钥，解决了攻击者可以假冒CA产生有效公钥认证的问题。在Tseng的认证加密方案，CA对用户公钥的证明没有使用CA的私钥，攻击者只要知道CA的签名等式，就可以假冒CA的签名。而本文的认证过程引入了CA的私钥，由于攻击者不知道CA的私钥，就不能产生有效的签名。只有CA才能使用私钥产生有效的签名。    同时，本方案的消息签名改正了Tseng的认证加密方案的缺陷。在tseng的认证加密签名方案中， r₁和 r₂具有线性关系，由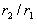 可以得到g^k，且可以恢复消息M。本文提出的签名方案，计算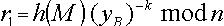，避免 r₁和 r₂形成线性关系，当攻击者截取签名（r₁ ,r₂ , s）后，不能由r₁ 和 r₂得到g^k ，因此不能恢复消息M。

5  结论

    本文的公钥自证明方案，实现了用户匿名注册、双向身份认证、数字签名以及消息恢复和验证。该方案与Tseng提出的方案相比，使用认证中心的私钥产生公钥，防止攻击者伪造公钥证明；而且改进了Tseng方案中攻击者可以伪造用户签名的缺点。同时，用户的身份证明在消息恢复和认证过程中实现，没有单独的用户身份认证阶段，减少了通信次数和信息量，很好地实现了通信双方的身份证明，有效地解决了密钥管理和密钥分发地问题，能够防止内部攻击，而需要的存储空间、通信量和计算量都很少，在IC卡、通信等领域有广泛的应用前景。

文献

[1] Nyberg K, Rueppel RA. Message recovery for signature schemes on the discrete logarithm [A] .In: Perugia. pre-proceedings of Eurocyp’94[C].Italy,1994.175～190[2] Lee WB, Chang CC, Yang WP. Authenticated encryption schemes without using it one way function [J]. Electron letter．1995,31(19)：1656～165[3]A Shamir. Identify-based cryptosystem based on the discrete logarithm problem[C]. In: Advances in cryptology-Eurocrypt’ 84,Springer，Berlin，1985:47~53 [4]M Girault. Self-certified public keys, LNCS 434 [C].In: Advances in cryptology: Proc.Eurocrypt’91, Springer, 1991: 490~497[5] Y Shang, T C Wu , S C Huang . ElGamal-like digital signature and multisignature schemes using self-certified public keys [J]. Journal of Systems and software, 2000;50(2):99~105[6] Y M Tseng, J K Jan , H Y Chien. Digital signature with message recovery using self-certified public keys and its variants [J]. Applied Mathematics and Computation, 2003; 136(2-3): 203~214[7] Jianhong Zhang, Hu'an Li. On the security of a digital signature with message recovery using self-certified public key [J]. Networking and Mobile Computing, 2005. Proceedings. 2005; 2(23~26): 1171 - 1174[８]. Networking and Mobile Computing, 2005. Proceedings. 2005; 2(23~26): 1171 - 1174