中小型乡镇企业绩效的DEA评价

摘 要 对中小型乡镇绩效评价的DEA模型(C2R)及应用进行了研究。通过DEA有效性分析，对乡镇企业绩效进行效率衡量，并对非DEA有效的决策单元进行投影改进，找出更有效的投入产出量，一定程度上为企业的投入产出量提供了依据，也为企业提高效率提供了数据借鉴。
　　 关键词 乡镇企业 综合评价 DEA C2R模型
1 前言
中小型企业的生产规模、投入资金等相对较少，为了合理地利用有限资源，使其最大限度地发挥作用，有必要对乡镇企业进行绩效评价。目前，对企业绩效进行综合评价的方法很多，多元统计分析、模糊数学、灰色系统理论、多维标度分析及空间统计学等方法也被成功使用，并取得了一定的效果。本文基于数据包络分析(Data Envelopment Analysis，简称DEA)给出乡镇企业绩效评价的一种方法。
数据包络分析(DEA)是由Charnes、Cooper在Farell测度基础上起来的一种评价决策单元(Decision Making Unit，DMU)相对绩效的非参数方法，它通过保持决策单元的输入或输出不变，借助数学规划将DMU投影到DEA前沿面上，并通过比较决策单元偏离DEA前沿面的程度来评价它们的相对有效性，是估计多输入与多输出及多目标决策类问题的有力工具。此方法已广泛应用于运输、、军事、政府机构、能源、农业及高科技研发部门等各层面。近年来，DEA应用于营利事业单位评估者亦有逐渐增多的趋势。
2 DEA评价模型
2.1 企业绩效评价的DEA方法及特点
将评价对象中小型乡镇企业视作DEA的DMU，对具有类似生产特征和管理属性的若干中小型乡镇企业进行绩效综合评价，通过其技术指标判断DMU是否对DEA有效，本质上是判断DMU是否位于生产可能集的前沿面上。使用DEA对DMU进行绩效评价时，由于DEA方法对输入、输出指标有较大的包容性，可以接受那些在一般意义下很难定量的指标，因此，它在处理评价问题时比一般常规统计方法更有优越性。首先，DEA方法可以同时企业的多种输入和输出数据，且这些数据的量纲并不要求一致；其次，在无需主观对企业经济指标赋权条件下，估计出确实有效的生产前沿面，能有效区分有效与非有效；第三，在对每个评价企业进行优化的基础上，不仅可以排序，还可提供具体改进建议。
2.2 企业绩效评价的DEA模型
假设有n个评价企业DMU，每个DMU都有m种输入指标及s种输出指标，对应的权系数分别为v=（v1，v2，……，vm）T和u=（u1，u2，……，us）T。
每个决策单元都有相应的效率评价指数：
hj=■=■，j=1，2，…，n（1）
适当地选取u和v，使其满足hj≤1。现对第j0个评价企业进行绩效评价，则以第j0个评价对象的效率指数为目标，以所有评价企业的效率指数为约束，其最优化模型为：
（P）max■=v■s.t.■≤1 j=1，…，nuk≥0 k=1，…，svi≥0 i=1，…，m（2）
模型（P）即为原始的C2R模型，它是一个分式规划问题，其含义为在其他DMU的产出投入比一定条件下DMU0的产出投入比要达到最大。利用 Charness-Cooper变换和对偶规划理论，并引入非阿基米德无穷小量的概念，可以将模型（P）化为等价并在实际评价中常用的线性规划模型。
（Dε）min［θ-ε（e■s■+■■s■）］=V■s.t.■λ■x■+s■=θ■■λ■y■+s■=y■λ■≥0，j=1，…，ns■≥0，s■≥0（3）
其中■=（1，…，1）T∈Rm，e=（1，…，1）T∈Rs，ε为非阿基米德无穷小量，s-是与投入相对应的松弛变量的向量，s+是与产出相对应的剩余变量的向量。
2.3 C2R模型的规模效益分析
设Dε有最优解λ■■(i=1,2,…，n)，记k=■λ■■，称k为DMUj0的规模效益值。当k=1时，表示DMUj0的规模效益不变，此时DMUj0达到最大产出规模点；当k<1时，表示规模效益递增，且k值越小规模效益递增趋势越大，表明DMUj0在投入Xj0的基础上适当增加投入量，产出量将有更高比例的增加；当k>1时，表示规模效益递减，且k值越大规模效益递减趋势越大，表明DMUj0在投入Xj0的基础上增加投入量不可能带来更高比例的产出。
2.4 综合评价
设规划问题（Dε）的最优解为λ*，s-*，s+*，θ*，则：
（1）当θ=1且s-=s+=0时，称DMUj0为DEA有效，即规模和技术有效，即在这n个决策单元组成的系统中，在原投入Xj0的基础上获得的产出Yj0已达到最优。
（2）当θ=1且s-≠0或s+≠0时，称DMUj0为DEA弱有效，即在这n个决策单元组成的系统中，投入Xj0可减少而保持产出的Yj0不变，或在投入Xj0不变的情况下将产出提高。
（3）当θ<1时，称DMUj0为DEA无效，即在这n个决策单元组成的系统中，可通过组合将投入降至原投入Xj0的θ比例而保持原产出Yj0不减少。
3 应用研究
3.1 评价指标体系
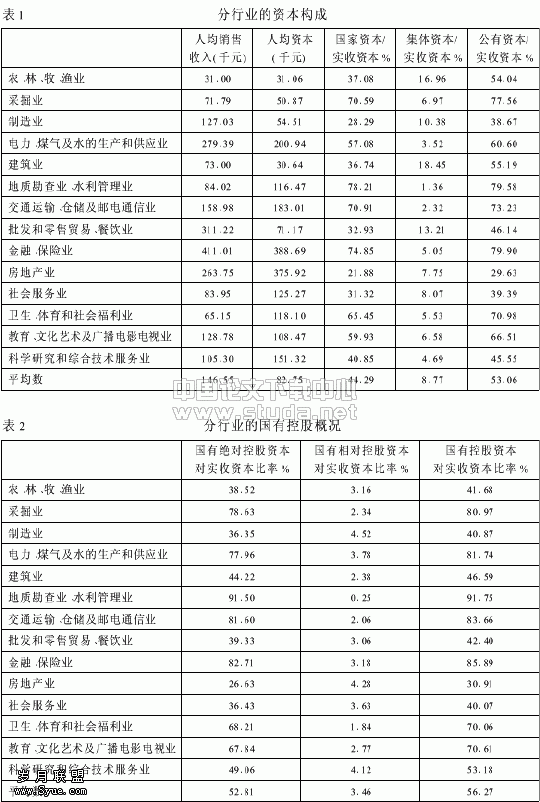
这里以某市8个规模、类型相近的中小型乡镇的投入产出情况为例来说明DEA中C2R模型的具体应用。在应用C2R模型前先要确定评价对象DMU是否具有相同的属性，即各个DMU要有相同的投入产出指标。其次在实际应用时，可根据需要选择指标数量，对于本例的乡镇企业来说，选投入指标为：X1为从业人员(人)，X2为中间投入（万元），X3为平均资产总额（万元），X4为年折旧及大修费（万元）；选产出指标为：Y1为营业收入（万元），Y2为利润总额（万元），Y3为上缴税金（万元），Y4为总产值（万元）。研究企业的技术指标见表1。
3.2 企业评价
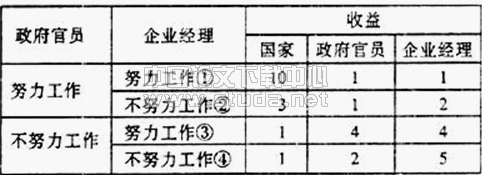
将原始数据带入模型（Dε），并用解线性规划模型的软件LINDO求解，得出的结果见表2。
3.3 非相对有效评价企业的改进方向
由表2可得，评价企业中企业A1~A6是相对有效的，而企业A7、A8是非相对有效的。
对非DEA有效的DMUj0，可借助投影分析将其改进为具有DEA有效性的决策单元。设
X′j0=θ*Xj0-s-*，Y′j0=Yj0+s+*（4）
其中，s-*，s+*，θ*是决策单元对应的线性规划问题的最优解，则（X′j0，Y′j0）为DMUj0对应的在DEA的相对有效面上的“投影”，是DEA有效的，这为改进非有效的DMU提供了一个可行方案。按式（4）的企业A7、A8的改进值见表3。
3.4 结果讨论
从以上评价计算结果可以得出：前6个企业属于DEA相对有效，而后两个企业有改进的余地，减少投入的资金和人数，但产出却可以增加。第1、2、5个企业的经济实力相对较弱，这一点可从投入的数据看出，他们能达到规模有效状态，说明经济系统的效率不仅取决于生产要素本身的水平，还取决于要素的合理组合应用，因此经济实力相对较弱的企业如能将自己有限的条件合理地组合利用，也能达到较高地生产效率。第7个企业的生产效率相对最差。由于第7个企业的生产规模较大，从业人员、中间投入、平均资产都是最多的，这种低效率生产显然不能适应企业的健康发展。
4 结论
应用DEA模型对中小型乡镇企业绩效进行分析评价，方法简便易行，且具有较强的适用性，评价结果具有较高的可靠性。它仅需要由决策单元投入产出指标组成的状态可能集满足凸性、无效性及最小性即可。通过模型求解以及有效性及改进分析，能获得企业更多的信息，不但为投资者理性投资提供依据，而且还能为企业本身提高其经营业绩提供可靠的数据借鉴。
该模型通过评价对象的多投入、多产出指标对企业绩效进行评价，其结果为评价对象相对评价集的相对有效性。为此，选择合理的评价集将直接影响评价对象的评价结果，在实际应用中，对评价值需按行业一般标准或按评价目的的要求，对评价集进行筛选，这样得到的评价结果将会更加符合实际，更有指导意义。

1 伍海华，马媛. 上市公司业绩的DEA有效分析—以青岛市为例[J]. 山东经济，2003（2）
2 张目. 基于DEA模型的GIS工程技术开发方法的综合评价[J]. 武汉大学学报，2004（1）
3 盛昭瀚，朱乔，吴广谋. DEA理论、方法与应用 [M].北京：出版社，2003
4 陈军飞，严以新. 水运业效率DEA评价研究[J].河海大学学报（科学版），2004（4）